Question 1207781: A bathroom tub will fill in 15 minutes with both faucets open and the stopper in place. With both faucets closed and the stopper removed, the tub will empty in 20 minutes. How long will it take for the tub to fill if both faucets are open and the stopper is removed?
My equation is this:
(x/15) + (x/20) = 1
You say?
Found 7 solutions by josgarithmetic, ikleyn, math_tutor2020, MathTherapy, greenestamps, Edwin McCravy, mccravyedwin:
Answer by josgarithmetic(39631)   (Show Source): (Show Source):
Answer by ikleyn(52932)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A bathroom tub will fill in 15 minutes with both faucets open and the stopper in place.
With both faucets closed and the stopper removed, the tub will empty in 20 minutes.
How long will it take for the tub to fill if both faucets are open and the stopper is removed?
~~~~~~~~~~~~~~~~~~
Your equation is incorrect.
In this problem, there are two opposite processes.
One process is filling with the rate of 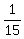 of the volume per minute
(two faucets combined).
Another process is draining with the rate of the volume per minute
(two faucets combined).
Another process is draining with the rate  of the volume per minute.
So, when both facets are open and the stopper is removed, the net filling rate is the difference of the volume per minute.
So, when both facets are open and the stopper is removed, the net filling rate is the difference
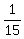 - -  = = 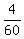 - -  = =  of the volume per minute.
It means that the filling process will take 60 minutes, or 1 hour. ANSWER of the volume per minute.
It means that the filling process will take 60 minutes, or 1 hour. ANSWER
Thus, the problem is just solved (mentally).
If you want to write an equation, you should formalize this reasoning.
Let "t" be the time to fill, in minutes.
Then in t minutes, the two facets will fill  part of the volume,
while through the stopper hole, the part of the volume,
while through the stopper hole, the  part of the volume will be removed.
The volume will be fully filled when part of the volume will be removed.
The volume will be fully filled when
 - -  = 1 (the whole volume).
Write with common denominator and find t = 1 (the whole volume).
Write with common denominator and find t
 - -  = 1, = 1,
 = 1,
t = 60*1 = 60 minutes.
ANSWER. The required time is 60 minutes, or 1 hour. = 1,
t = 60*1 = 60 minutes.
ANSWER. The required time is 60 minutes, or 1 hour.
Solved.
--------------------
To see many other similar (and different) introductory problems on joint work,
solved with complete explanations to teach you, look into the lessons
- Using Fractions to solve word problems on joint work
Read it and get be trained in solving joint-work problems.
Consider this lesson as your textbook, handbook, guidebook, tutorials and (free of charge) home teacher,
which is always with you to help and to inspire.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
15*20 = 300
Consider a 300 gallon bathtub. It turns out this volume doesn't really matter. There's nothing special about the 300. You can pick any other positive number and the final answer will be the same at the end.
The 300 gallon tub fills up completely in 15 minutes if both faucets are on and the drain is closed.
I'll assume that the tub starts off completely empty in this scenario.
The fill rate is 300/15 = 20 gallons per minute.
rate = amountDone/time
When both faucets are off and the drain is open, the 300 gallon tub empties in 20 minutes.
I'll assume that the tub is completely full at the starting point of this scenario.
drain rate = 300/20 = 15 gallons per minute
Now let's consider the scenario where both faucets are on and the drain is open at the same time. It's an unfortunate waste of water.
In this situation, the fill rate and drain rate basically play a game of tug-of-war.
The fill rate wins out ultimately since the fill rate is larger compared to the drain rate (20 > 15).
The net fill rate is 20-15 = 5 gallons per minute.
Despite the drain wanting to remove the water, the faucets win out at the end of the day. Though of course it will take a bit longer to fill the tub.
How long would it take for the tub to completely fill up in this case?
rate*time = amountDone
time = amountDone/rate
time = (300 gallons)/(5 gallons per min)
time = 60 minutes
time = 1 hour
Answer by MathTherapy(10559)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A bathroom tub will fill in 15 minutes with both faucets open and the stopper in place. With both faucets closed and the stopper removed, the tub will empty in 20 minutes. How long will it take for the tub to fill if both faucets are open and the stopper is removed?
My equation is this:
(x/15) + (x/20) = 1
You say?
NOPE.....WRONG!!
Let T be the time it takes to fill the tub, when both faucets are turned on and the stopper is removed
The 2 faucets, when turned on, can FILL the tub in 15 minutes, or FILL 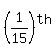 of tub in 1 minute
Also, the stopper, when removed, can cause the tub to EMPTY in 20 minutes, or cause of tub in 1 minute
Also, the stopper, when removed, can cause the tub to EMPTY in 20 minutes, or cause 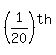 of tub to EMPTY in 1 min
We then get the following COMPLETE-JOB equation: of tub to EMPTY in 1 min
We then get the following COMPLETE-JOB equation:  Time it takes to fill the tub, when both faucets are turned on and the stopper is removed,
or T = 1 ÷
Time it takes to fill the tub, when both faucets are turned on and the stopper is removed,
or T = 1 ÷  = 1(60) = 60 minutes = 1(60) = 60 minutes
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Most of the responses you have received show some form of the standard algebraic solution, using the fact that the two faucets together fill 1/15 of the tub in 1 minute and the drain empties 1/20 of the tub in 1 minute.
Here is a solution by an alternative method for solving this kind of "working together" problem.
Consider the least common multiple of the two given times: the LCM of 15 and 20 is 60.
In 60 minutes, the two faucets could fill the tub 60/15 = 4 times; in 60 minutes, the drain could empty the tub 60/20 = 3 times.
So in 60 minutes the two faucets and the drain together could fill the tub 4-3 = 1 time.
ANSWER: 60 minutes
Answer by Edwin McCravy(20066)   (Show Source): (Show Source):
Answer by mccravyedwin(409)   (Show Source): (Show Source):
You can put this solution on YOUR website! A bathroom tub will fill in 15 minutes with both faucets open and the stopper in
place.There are 4 15-minute periods in an hour, so in an hour the faucets will
have poured out 4 tub-fulls of water. With both faucets closed and the stopper removed, the tub will empty in 20
minutes.There are 3 20-minute periods in an hour, so in an hour the unstopped hole will
have drained out 3 tub-fulls of water. How long will it take for the tub to fill if both faucets are open and the
stopper is removed?So in an hour, 4 tub-fulls of water will have been poured into the tub, and 3
tub-fulls of water will have drained out of the tub, so just enough water will
remain to fill up 4-3=1 tub-full.Answer: 1 hour.
Edwin
|
|
|