Question 1189275: Hector, Kenny and Elliot went shopping with $2190. Kenny spent $80 and Hector spent 2/5 of his money. Hector spent half as much as Elliot and had $160 less than what Elliot had left. In the end, Kenny and Hector had the same amount of money left. How much money had Elliot at first?
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hector, Kenny and Elliot went shopping with $2190.
Kenny spent $80 and Hector spent 2/5 of his money.
Hector spent half as much as Elliot and had $160 less than what Elliot had left.
In the end, Kenny and Hector had the same amount of money left.
How much money had Elliot at first?
~~~~~~~~~~~~~~~~~
This problem has unexpectedly twisted formulation (which is a rare case in such problems).
So, the major step forward is to algebraize it.
Let H, K and E be the amounts the persons had originally.
First equation is obvious
H + K + E = 2190. (1)
Hector spent 2/5 of his money; so, he left with 3/5 of his money.
Kenny spent $80; so Kenny left with (K-80) dollars.
At the end, Kenny and Hector had the same amount, which gives us the second equation
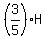 = K - 80
or
3H = 5K - 400. (2)
Hector spent half as much as Elliot, which means that Elliot spent twice as much as Hector.
Hence, Elliot spent = K - 80
or
3H = 5K - 400. (2)
Hector spent half as much as Elliot, which means that Elliot spent twice as much as Hector.
Hence, Elliot spent 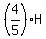 .
It means that Elliot left with E - .
It means that Elliot left with E - 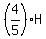 dollars.
From the problem, at the end Hector had left $160 less than what Elliot had left.
It gives us the last, third equation dollars.
From the problem, at the end Hector had left $160 less than what Elliot had left.
It gives us the last, third equation
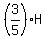 + 160 = E - + 160 = E - 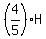 ,
or
7H - 5E = -800. (3)
Thus we have the system of 3 equations in 3 unknowns
H + K + E = 2190. (1)
3H - 5K = 400. (2)
7H - 5E = -800. (3)
So the problem is algebraized.
As I said at the beginning, the major step is to algebraize; solving the system is just technical part.
So, I used one of many existing online solvers www.reshish.com to save my time,
and I got this ANSWER : H= 650; K = 470; E = 1070. ,
or
7H - 5E = -800. (3)
Thus we have the system of 3 equations in 3 unknowns
H + K + E = 2190. (1)
3H - 5K = 400. (2)
7H - 5E = -800. (3)
So the problem is algebraized.
As I said at the beginning, the major step is to algebraize; solving the system is just technical part.
So, I used one of many existing online solvers www.reshish.com to save my time,
and I got this ANSWER : H= 650; K = 470; E = 1070.
Solved.
|
|
|