SOLUTION: A chord of a circle of diameter 10 feet is decreasing in length 1 foot per minute. Find the rate of change of the smaller arc subtended by the chord when the chord is 8 feet long.

The diameter is 10 ft., so the radius is 5 ft.
Let the arc at the top be "s".  We will need the formula 
, 
,

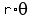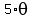and its derivative with respect to time t:



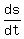
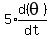Let the length of the chord be x. Since it is decreasing in length 1 foot per
minute, taken negative since it is decreasing.





Next we have to find an equation for x in terms of the chord and θ.  So we draw
this green line perpendicular to the chord, which bisects the chord and θ
and gives us two congruent right triangles.



From the right triangle,







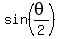
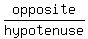
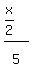
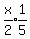
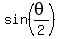
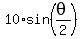Take the derivative with respect to time t:





Since 



We redraw the figure at the instant when the chord x = 8, which
makes the left half of it 4.  And since it's a 3-4-5 right triangle,
the green line is 3.





Since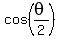 







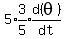
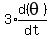
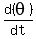Finally we substitute in









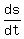
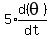
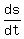
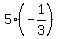
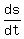
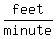
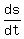
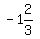
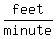The negative sign indicates that the arc is decreasing

Edwin