Question 1054626: Use the vertex
(h, k)
and a point on the graph
(x, y)
to find the general form of the equation of the quadratic function.
(h, k) = (−5, −1), (x, y) = (−7, 3)
f(x) = ________
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! Some of the description should be changed. Okay to let vertex be (h,k), but for some other given point on the graph, say this is some "given" point of something like (p,v). You do not want to confuse general point (x,y) with any specific point.
That now taken care of, start with Standard Form.
 , for some real number m so that  .
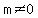Your graph for the equation passes through some given point, (p,v).
 -------Now you would "know" value for m.
Put everything back into the standard form.
Obviously this is not yet in GENERAL form, but still in fairly standard form. Just do all the needed "simplifications" or multiplications and arrange into general form.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
Use the vertex
(h, k)
and a point on the graph
(x, y)
to find the general form of the equation of the quadratic function.
(h, k) = (−5, −1), (x, y) = (−7, 3)
f(x) = ________
Vertex/Standard form: 
 ------ Substituting (- 7, 3) for (x, y) and (- 5, - 1) for (h, k)
 _____ ______ ______1 = a
Vertex/Standard form:  ______
|
|
|
