This Lesson (Calculations with fractions) was created by by ikleyn(52754)   : View Source, ShowAbout ikleyn:
Calculations with fractions
Problem 1a) Calculate  - -  . ----> Rewrite the fractions with the least common denominator, which is . ----> Rewrite the fractions with the least common denominator, which is  = =  , and then distract the numerators: , and then distract the numerators:  - -  = =  - - 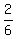 = =  = =  . .
b) Calculate  - -  . ----> Rewrite the fractions with the least common denominator, which is . ----> Rewrite the fractions with the least common denominator, which is  = =  , and then distract the numerators: , and then distract the numerators:  - -  = =  - - 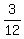 = =  = =  . .
c) Calculate  - -  . ----> Rewrite the fractions with the least common denominator, which is . ----> Rewrite the fractions with the least common denominator, which is  = =  , and then distract the numerators: , and then distract the numerators:  - -  = = 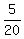 - - 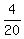 = =  = =  . .
d) Calculate  - -  . ----> Rewrite the fractions with the least common denominator, which is . ----> Rewrite the fractions with the least common denominator, which is  = =  , and then distract the numerators: , and then distract the numerators:  - -  = = 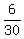 - -  = = 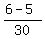 = =  . .
e) Calculate  - -  . ----> Rewrite the fractions with the least common denominator, which is . ----> Rewrite the fractions with the least common denominator, which is  = =  , and then distract the numerators: , and then distract the numerators:  - -  = = 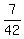 - -  = =  = =  . .
Problem 2Calculate  + +  + + 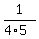 + + 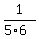 + +  . .
Solution
Surely, you can rewrite all the fractions with the common denominator and then add numerators. It is a boring way and it requires tons of calculations.
Fortunately, you may apply another trick. Look in the previous Problem 1 and replace  = =  - -  , ,  = =  - -  and so on. Then you can write and so on. Then you can write
 + +  + + 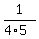 + + 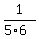 + +  = ( = ( - -  ) + ( ) + ( - -  ) + ( ) + ( - -  ) + ( ) + ( - -  ) + ( ) + ( - -  ). ).
Now, cancel all internal terms that have the opposite signs. You will get
 + +  + + 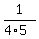 + + 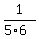 + +  = =  - -  = = 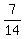 - -  = =  = = 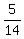 . .
My congratulations!!!
Problem 3a) Calculate  - -  . ----> Rewrite the fractions with the least common denominator, which is . ----> Rewrite the fractions with the least common denominator, which is  = =  , and then distract the numerators: , and then distract the numerators:  - -  = =  - -  = = 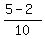 = =  . .
b) Calculate  - -  . ----> Rewrite the fractions with the least common denominator, which is . ----> Rewrite the fractions with the least common denominator, which is  = =  , and then distract the numerators: , and then distract the numerators:  - -  = =  - - 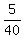 = =  = = 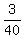 . .
c) Calculate  - -  . ----> Rewrite the fractions with the least common denominator, which is . ----> Rewrite the fractions with the least common denominator, which is  = =  , and then distract the numerators: , and then distract the numerators:  - -  = =  - - 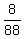 = =  = =  . .
d) Calculate  - -  . ----> Rewrite the fractions with the least common denominator, which is . ----> Rewrite the fractions with the least common denominator, which is 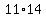 = =  , and then distract the numerators: , and then distract the numerators:  - -  = = 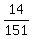 - - 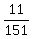 = =  . .
e) Calculate  - -  . ----> Rewrite the fractions with the least common denominator, which is . ----> Rewrite the fractions with the least common denominator, which is  = =  , and then distract the numerators: , and then distract the numerators:  - -  = =  - - 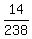 = = 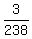 . .
Problem 4Calculate  + + 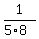 + +  + +  + + 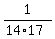 . .
Solution
You may apply the trick similar to that of the Problem 2 above. Look in the previous Problem 3 and replace  = =  .( .( - -  ), ), 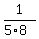 = =  .( .( - -  ) and so on. Then you can write ) and so on. Then you can write
 + + 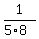 + +  + +  + + 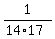 = =  . [ ( . [ ( - -  ) + ( ) + ( - -  ) + ( ) + ( - -  ) + ( ) + ( - -  ) + ( ) + ( - -  ) ]. ) ].
Now, cancel all internal terms that have the opposite signs. You will get
 + + 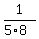 + +  + +  + + 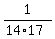 = =  .( .( - -  ) = ) =  .( .(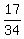 - - 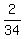 ) = ) =  . . = =  . .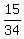 = =  . .
The problem is solved!
Problem 5Calculate 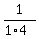 + +  + +  + +  + +  . .
Solution
Just touched by the solution of the Problem 4, you may suggest that 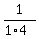 = =  .( .( - -  ), ),  = =  .( .( - -  ) and so on. It is true. Indeed, ) and so on. It is true. Indeed,
 - -  = = 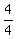 - -  = = 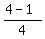 = =  , ,
 - -  = =  - -  = =  = =  , ,
 - -  = =  - -  = = 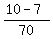 = =  , ,
 - -  = = 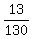 - -  = = 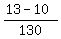 = = 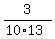 , ,
 - -  = =  - - 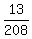 = = 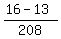 = =  . .
Having this, you can write
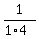 + +  + +  + +  + +  = =  . [ ( . [ ( - -  ) + ( ) + ( - -  ) + ( ) + ( - -  ) + ( ) + ( - -  ) + ( ) + ( - -  ) ]. ) ].
Now, cancel all internal terms that have the opposite signs. You will get
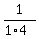 + +  + +  + +  + +  = =  .( .( - -  ) = ) =  . . = =  . .
Problem 6Calculate  + +  + +  + +  + +  on your own. on your own.
Problem 7Simplify  + + 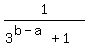 . .
Solution
Let x =  , for brevity.
Then , for brevity.
Then 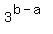 = =  .
So, .
So,  + + 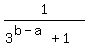 = =  + +  = =  + + 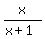 = = 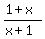 = 1. ANSWER = 1. ANSWER
My other lessons on fractions in this site are
- Using fractions to solve word problems
- Using fractions to solve Travel problems
- Advanced problems on ratios
- Entertainment problems on fractions
- OVERVIEW of my lessons on fractions
This lesson has been accessed 3942 times.
|

