Questions on Algebra: Number Line answered by real tutors!

Tutors Answer Your Questions about Number-Line (FREE)

Question 1209726: Which is the result of multiplying all positive divisors of 2016?
a) 2016^19
b) 2016^16
c) 2016^18
d) 2016^17
e) 2016^15
Answer by math_tutor2020(3817)

(Show Source):

You can put this solution on YOUR website!

Answer: 2016^18 which is choice C

Explanation

2016 = 2^5*3^2*7
d(n) = number of divisors of n
a,b,c = positive integers
p,q,r = primes
d(p^a*q^b*r^c) = (a+1)*(b+1)*(c+1) .... see formula (3) of this page and see this page
d(2^5*3^2*7^1) = (5+1)*(2+1)*(1+1)
d(2016) = 36

The value 2016 has 36 divisors.
Verification using WolframAlpha
There are many other online calculators that will perform a similar function.

The divisors pair up to multiply to 2016
Eg: 2*1008 = 2016 and 8*252 = 2016

Those 36 divisors form 36/2 = 18 copies of 2016 multiplied together when multiplying all the positive divisors.
Therefore we arrive at the answer 2016^18
This massive number is approximately 3.0257 * 10^59
It is roughly 30257 followed by 55 copies of 0.

Question 1208311: How many intergers between 31 and 131 are divisible by 7 but not divisible by 6?
Found 4 solutions by greenestamps, MathTherapy, ikleyn, math_tutor2020:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

The range is 100, from 31 to 131; and neither 31 nor 131 is divisible by 7. So the number of integers divisible by 7 in the given range is 100/7 = 14 (and a fraction that we don't care about).

The numbers in the given range that are divisible by both 7 and 6 are the multiples of 7*6 = 42. In the given range, there are 3 such numbers: 42, 84, and 126.

So the number of integers in the given range that are divisible by 7 but not by 6 is 14-3 = 11.

ANSWER: 11

Answer by MathTherapy(10552)   (Show Source):
You can put this solution on YOUR website!

How many intergers between 31 and 131 are divisible by 7 but not divisible by 6? We start with Since 28 is SMALLER than 31, we ADD 7 to 28 to get 28 + 7 = 35, the SMALLEST INTEGER between 31 and 131, that is DIVISIBLE by/is a MULTIPLE of 7. We then continue with Since 126 is SMALLER than 131, we get 126 as the LARGEST INTEGER between 31 and 131, that is DIVISIBLE by/is a MULTIPLE of 7. So, ALL INTEGERS between 31 and 131, that are DIVISIBLE by/are MULTIPLES of 7, begin at 35 and end at 126. So, the TOTAL number of INTEGERS, between 31 and 131, that are DIVISIBLE by/are MULTIPLES of 7, is INTEGERS between 31 and 131, that are DIVISIBLE by both 7 and 6, start at 7(6) = 42. We then continue with Since 126 is SMALLER than 131, we get 126 as the LARGEST INTEGER between 31 and 131, that is DIVISIBLE by/is a MULTIPLE of 42. So, the TOTAL number of INTEGERS between 31 and 131, that are DIVISIBLE by/are MULTIPLES of 7 and 6, or 42, is TOTAL number of INTEGERS between 31 and 131, that are DIVISIBLE by/are MULTIPLES of 7, but are NOT DIVISIBLE by/are NOT MULTIPLES of 6 (or 42) = 14 - 3 = 11

Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website!
.
How many integers between 31 and 131 are divisible by 7 but not divisible by 6?
~~~~~~~~~~~~~~~~~~~~~~

In the interval between 31 and 131, first integer number divisible by 7 is 35, and they go with the step of 7 to the last integer divisible by 7, which is 126. From 35 to 126, there are 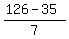+ = 14 integer numbers divisible by 7. From this number 14, we should subtract the number of those integers that are divisible by both 6 and 7 simultaneously. These integers are divisible by 42, too, and their number is 3, because there are 3 (three) such integer numbers 42, 84 and 126. So, we subtract 3 from 14, and we get the ANSWER. Between 31 and 131, there are 14-3 = 11 integers that are divisible by 7 but not divisible by 6.

Solved.

Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
31/7 = 4.4286
7*4 = 28 is too small but 7*5 = 35 fits
131/7 = 18.7143
7*18 = 126 also fits
7*19 = 133 is too large.

The multiples of 7 between 31 and 131 are: {35, 42, 49, ..., 126}
They can be written as {7*5, 7*6, 7*7, ..., 7*12, ..., 7*18}

Cross off 7*6, 7*12 and 7*18 since they involve 6 as a factor.
There are 14 items in the set {5,6,7,...,18} because 18-5+1 = 14. Or you can count out the items.
That must mean there are also 14 items in the set {7*5,7*6,...,7*18} = {35,42,...,126}
We crossed off 3 items {7*6,7*12,7*18} so we have 14-3 = 11 multiples of 7 between 31 and 131 such that 6 isn't a factor.

Answer: 11

Question 1208135: Mauna Kea, a dormant shield volcano on the island of Hawai’i, is the
state’s highest point at 13,803 feet above sea level. A large portion of
the volcano is below sea level, so when measured from the ocean
floor, its total height is 33,100 feet.
Which distance is greatest and by how many feet?
Ⓐ the distance between the peak of Mauna Kea and sea level; by
13,803 feet
Ⓑ the distance between the peak of Mauna Kea and sea level; by
33,100 feet
Ⓒ the distance between the base of Mauna Kea on the ocean floor
and sea level; by 19,297 feet
Ⓓ the distance between the base of Mauna Kea on the ocean floor
and sea level; by 13,803 feet
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website!
.

Similar question can be found in a composition "Gargantua and Pantagruel" of the famous French writer
François Rabelais (16th century)

    - If you had to travel to Cahusac, what would you prefer - to ride a goose or to pull a pig on a string?

Question 1208086: Numbers a and b are located to the
left of c on a number line. Select all
the inequalities that could be true.
A a < b < c
B b < c < a
C c < a < b
D a = b and b < c
E b < a < c
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

a and b are both to the left of c on the number line. So, when the inequalities are written in the standard form, with the smaller numbers to the left (as all the answer choices are), then c must be the last (rightmost) number in the inequality. Furthermore, the inequality must end with "... < c".

So answer choices B and C are not possible.

The given information says nothing about the relationship between a and b, so answer choices A, D, and E are all possible.

ANSWER: A, D, E

Question 1207471: Let p and q be two positive numbers where p > q. Geoffrey graphs
the numbers p, q, and their opposites on a number line. Which
statements must be true for all values of p and q?
Select all that apply.
A The number − q lies halfway between 0 and − p.
B The number − q is greater than the number − p.
C The number − p is closer to 0 than is − q.
D The number 0 is between − p and − q.
E The number q is closer to 0 than − p.
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

Draw a number line with the numbers 0, p, q, -p, and -q as prescribed and answer the questions yourself....

Note you might need to draw 2 or 3 such number lines with different values for p and q to answer the question correctly.
...-----|------|---|---|------|-----... -p -q 0 q p or... ...------|---|---------|---------|---|------... -p -q 0 q p

A: Is the number − q halfway between 0 and − p on both number lines?
B: Is the number − q greater than the number − p on both number lines?
C: Is the number − p closer to 0 than − q on both number lines?
D: Is the number 0 between − p and − q on both number lines?
E: Is the number q closer to 0 than − p on both number lines?

Question 1206309: How to represent -2+(-7) on a number line
Found 2 solutions by math_tutor2020, Solver92311:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!

Some students may prefer horizontal number lines.
Other students may prefer vertical number lines.

If you like the 1st option, then start at -2.
Then move 7 units left to arrive at -9

If you prefer a vertical number line, then start at -2 and move down 7 units to arrive at -9.

Here are some real world applications of how to interpret -2 + (-7) = -9
You are 2 meters under the ocean's surface. Going down another 7 meters will produce a final depth of 9 meters below the surface.
Your car is parked on the basement 2 level (B2) of a parking garage. Your friend parked his car 7 floors beneath yours, so his car is on level B9.
The temperature is -2 degrees C. After the temperature lowers by 7 degrees, it is now -9 degrees C.
You are 2 dollars in debt. This is represented by -2. Borrowing 7 more dollars brings the total debt to $9

Answer by Solver92311(821)   (Show Source):
You can put this solution on YOUR website!

Start at 0.

Go left two units. That puts you at -2

Go left seven more units. That puts you at -9

John

My calculator said it, I believe it, that settles it

From
I > Ø

Question 1206100:
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website!
Please post a question. I cant see it

Question 1206088: Locate and label 7/6 on a number line 0————1————-2
Found 2 solutions by josgarithmetic, MathLover1:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!
Think about it.
7/6 is greater than 1 and less than 2.
.
.
You can do this without anyone's help.

Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!

Question 1205654: Plot the numbers 3/2 and -1 3/4 on number line
Found 3 solutions by math_tutor2020, josgarithmetic, MathLover1:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!

3/2 = 1.5 will go at the midpoint of 1 and 2.

-1 & 3/4 = -1.75 will go between -2 and -1
Split the interval from -2 to -1 into 4 equal pieces.
Then mark the quarter position closest to -2.

In other words, let's say A,B,C are at -2, -1.5, and -1 respectively.
B is the midpoint of A and C.
The location of -1.75 is at the midpoint of A and B

Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!

Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!
and on number line

Solved by pluggable solver: Plotting Numbers on a Number Line

Question 1205268: What number is in between -2 and -0.75

Found 3 solutions by ikleyn, math_tutor2020, MathLover1:
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website!
.

One small correction to the post by @math_tutor2020.

Traditionally, geometric mean is defined for positive numbers, ONLY.

See this source (Wikipedia article)
https://en.wikipedia.org/wiki/Geometric_mean

So, ignore the consideration in his post, that relates to geometric mean of the numbers -2 and -0.75.

The rest in that post is Ok.

Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!

There are infinitely many numbers between -2 and -0.75, but one number we could pick on is the midpoint.

Add up the values and then divide in half

Add: -2+(-0.75) = -2-0.75 = -2.75
Divide in half: -2.75/2 = -1.375
The value -1.375 is between -2 and -0.75
This is known as the arithmetic mean.

-----------------------------------------------------------------------------------

Or we could apply the geometric mean
Multiply the values and then apply the square root.

Multiply: -2*(-0.75) = 1.5
sqrt(1.5) = 1.2247 approximately
Make the result negative so it's in between the two negative values
-1.2247 approximately is between -2 and -0.75

Edit: @ikleyn, fair enough, the geometric mean approach seemed a bit flimsy. However, we could treat it like finding the geometric mean of 2 and 0.75 and then make the result negative.

-----------------------------------------------------------------------------------

Another thing we could do is find the distance between the given values
distance = |a-b| = |-2-(-0.75)| = |-2+0.75| = |-1.25| = 1.25
Then cut this distance into N pieces, let's say N = 10
1.25/N = 1.25/10 = 0.125

Let k be some integer on the interval 0 < k < N
In this case 0 < k < 10

Then let's add some multiple of 0.125 to the left endpoint -2, to land somewhere between -2 and -0.75
We're evaluating -2+0.125k for k = 1 through k = 9
If k = 1, then -2 + 0.125k = -2 + 0.125*1 = -1.875
If k = 2, then -2 + 0.125k = -2 + 0.125*2 = -1.75
If k = 3, then -2 + 0.125k = -2 + 0.125*3 = -1.625
If k = 4, then -2 + 0.125k = -2 + 0.125*4 = -1.5
If k = 5, then -2 + 0.125k = -2 + 0.125*5 = -1.375
If k = 6, then -2 + 0.125k = -2 + 0.125*6 = -1.25
If k = 7, then -2 + 0.125k = -2 + 0.125*7 = -1.125
If k = 8, then -2 + 0.125k = -2 + 0.125*8 = -1
If k = 9, then -2 + 0.125k = -2 + 0.125*9 = -0.875
Each of the results {-1.875, -1.75, -1.625, -1.5, -1.375, -1.25, -1.125, -1, -0.875} are between -2 and -0.75

Notes: If k = 0, then -2+0.125k = -2 is the left endpoint, while k = 10 means -2+0.125k = -0.75 is the right endpoint.

There's nothing special about N = 10. We could have easily made N = 20 or whatever positive whole number you want.

And yet another approach is to select the number -1 since it's between -2 and -0.75, and then tack on some random string of decimal digits.
Eg: -1.2345 or -1.6789

Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!

if a number is in between:

and are rational numbers, so there are infinitely many rational numbers between these two numbers
I am going to choose random number between and which is (one example)

Question 1201952: | - | - - | - - |
5 x y 3x
In the number line above, if the marks are equally spaced, what is the value of the coordinate y?
(A) 10
(B) 20
(C) 30
(D) 40
(E) 50
Found 3 solutions by greenestamps, josgarithmetic, ikleyn:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

To me, the problem is clear; and it IS a good math problem....
| - | - - | - - | 5 x y 3x

The distance from x to y is the same as the distance from y to 3x:

y-x = 3x-y
2y = 4x
y = 2x
| - | - - | - - | 5 x 2x 3x

Note we could also obtain that result by saying that y is halfway between x and 3x....

The distance between x and y (which is 2x) is twice the distance between 5 and x:

2x-x = 2(x-5)
x = 2x-10
x = 10

ANSWER: y = 2x = 2(10) = 20 Answer (B)

Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!
| - | - - | - - |
5 x y 3x

Cannot be read correctly shown that way.

If the MARKS are equally spaced, then maybe should be more like this:

| - - | - - | - - | 5 x y 3x

"Coordinate values"?

Could use this:

MEANINGLESS
MEANINGLESS

Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website!
.

What this post is about ?

If you think that you presented a Math problem here, then you make a mistake.

Question 1199656:
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website!
.

Your request was about plotting - - - so I deleted it immediately as I saw it.

This forum is not an art studio to make plots on requests of visitors.

It is intended for other purposes.

Question 1198494: Plot 1/12 and 2/56 on a number line
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website!
.

1/12 is here ----|--|----------------------|---- 0 1/12 1

Now you make 2/56 in the same way.

Another way to get 1/12 on a number line is THIS:

        take an inch ruler/(straightedge) and note first inch mark in the first foot interval.

        1 inch = 1/12 of a foot.

Question 1197964: use a number line to find each sum -3+4

Found 2 solutions by ewatrrr, josgarithmetic:
Answer by ewatrrr(24785)   (Show Source):
You can put this solution on YOUR website!
-3 + 4 Same As 4 +(- 3) = 1
to find sum: Start at 4 and count back 3 spaces

Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!
You can do this. Draw and label your number line. Start at -3. Move 4 units to the right (positive). What is the number there? It should be at +1.

Question 1196035: Refer to the number line. Find the coordinate of point Y such that the ratio of MY to YJ is 2:3.

Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

Obviously we can't help you find the answer, since you don't show us the number line.

But we can tell you how YOU can find the answer....

I will assume that point Y is between M and J; the solution method would be different if it were not.

Let the given points on the number line be M = a and J = b. Then here are two ways you can solve the problem.

(1) Use the given ratio to determine what fraction of the distance from M to J point Y is located. Then to find the coordinate of Y, add that fraction of the distance from M to J to the coordinate of M.

This possible sounds confusing, but if you use this method a couple of times, it should make sense.

The ratio MY:YJ is 2:3. That means Y is 2/(2+3) = 2/5 of the way from M to J. So to find the coordinate of Y, add 2/5 of the distance from M to J to the coordinate of M. The distance from M to J is (b-a), so

I'll pick some numbers for M and J to show a sample calculation by this method.

M = 7; J = 13
distance from M to J: 13-7 = 6
2/5 of the distance from M to J: (2/5)6 = 12/5 = 2.4
coordinate of Y: 7 + 2.4 = 9.4

(2) Treat the problem as a "mixture" problem.

It is harder to understand how this method works; but the required calculations are shorter. Many students like this method; but some find it too confusing.

Since the given ratio is 2:3, the coordinates of M and J must be "mixed" with 2 parts of one and 3 parts of the other. The confusing part to this method is that the ratio 2:3 means Y is closer to M than to J, so the "mixture" must use 3 parts of the coordinate of M and 2 parts of the coordinate of J.

So the calculation for the coordinate of Y is (3/5) of a plus (2/5) of b:

Using this method on the same example as above, with M = 7 and J = 13, the calculation is

Try both of these methods on your problem and see which "works" better for you.

Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website!
.
Refer to the number line. Find the coordinate of point Y such that the ratio of MY to YJ is 2:3.
~~~~~~~~~~~~~~~~~~~~

Makes no sense, as posted.

The key input info is LOST in this post.

Question 1195423: Find the equation for the line that passes through (8,3) that has slope -1. Give your answer in point slope form. You do not need to simplify.
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website!
.

    y-3 = (-1)*(x-8).         ANSWER

Solved.

-------------

Explanation on HOW TO do:

1) Since x-coordinate is 8, you write (x-8) in the right side. 2) Since y-coordinate is 3, you write y-3 in the left side. 3) Since the slope is -1, you use the factor (-1) at (x-8) in the right side.

It works for every/any/each similar problem.

. . . . . . . .

To see many other similar problems solved, look into the lesson
    - Equation for a straight line having a given slope and passing through a given point
in this site.

Learn the subject from there once and for all.

Question 1195349: Find the equation of the line passing those the points (10,-27) and (-10,-9). Write your answer in the form y=mx+b.
Found 2 solutions by MathLover1, josgarithmetic:
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!

Find the equation of the line passing those the points (,) and (,).
Write your answer in the form:
.......where is a slope and is -intercept

since given two points, use them to find a slope

.......the points are (,) and (,)

now use point slope equation
......substitute slope and given point (,)

-> your equation

Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!
Look at the previous example.. That is clear enough so you can figure how to do this one.

Question 1195320: Find an equation of the line that has a slope of 10 and a y intercept of (0,8). Write your answer in the form y = Mx + b

Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website!
.
Find an equation of the line that has a slope of 10 and a y intercept of (0,8).
Write your answer in the form y = Mx + b
~~~~~~~~~~~~~~~~

If the slope is m and y-intercept is the point (0,b), then a straight line equation of the form y = Mx + b is y = mx + b, or, in your case, y = 10x + 8. ANSWER

Solved, answered and explained.

-----------------

To see other similar solved problems (your future TEMPLATES), look into the lesson
    - Equation for a straight line having a given slope and passing through a given point
in this site.

Learn the subject from there.

Question 1194661: What is the probabilty of getting a sum of 9 from two throws of dice?
Select one:
a.
1 / 3

b.
1 / 6

c.
1 / 9

d.
1 / 4
Found 3 solutions by greenestamps, ikleyn, MathLover1:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

The solution from MathLover, as well as most of the examples on the link provided by tutor @ikleyn, solve the problem by looking at which outcomes in the sample space satisfy the given requirements. That is, of course, a valid way to solve a problem like this.

Another way to solve this kind of problem is to imagine rolling the two dice one at a time and considering the probability that each roll still makes it possible to get the desired end result.

For this problem, the sum of the two dice must be 9. Since the largest number on each die is 6, the outcome on the first die must be at least 3. The probability of that happening (die shows 3, 4, 5, or 6) is 4/6 = 2/3.

Then, once the first die has been rolled, for each number on the first die there is only 1 number on the second die that will give a sum of 9; so the probability of a "good" roll on the second die is 1/6.

Then the probability of a sum of 9 is the product of the probabilities of "good" outcomes on the rolls of both dice: (2/3)*(1/6) = 2/18 = 1/9.

Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website!
.

On rolling dice problems see the lesson
    - Rolling a pair of fair dice
in this site. You will find there many similar solved problems.

Read it and learn the subject from there. After that, you will be able easy solve such problems
ON YOUR OWN, which is your MAJOR GOAL visiting this forum (I believe).

Also, you have this free of charge online textbook in ALGEBRA-II in this site
    - ALGEBRA-II - YOUR ONLINE TEXTBOOK.

The referred lesson is the part of this online textbook under the topic "Solved problems on Probability".

Save the link to this textbook together with its description

Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson

into your archive and use when it is needed.

Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!

When two dice are rolled together then total outcomes are and
Sample space is
[ (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6)
(2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)
(3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6)
(4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)
(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)
(6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) ]
So, pairs with sum are (,) (, ) (, ) (, ) i.e. total pairs
Total outcomes =
Favorable outcomes =
Probability of getting the sum of 9 = Favorable outcomes / Total outcomes
=
So, P(sum of ) =.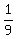

answer:
c.

Question 1194656: For the infinite geometric series below, identify whether it converges or diverges.
10, 5, 2.5, 1.25, ....

Select one:
a.
Diverges

b.
Both

c.
Neither

d.
Converges
Found 2 solutions by math_tutor2020, greenestamps:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!

Answer: D) converges

======================================================

How to find that answer:

We'll need the common ratio, denoted as r.

Pick any term and divide it over the previous term
r = term2/term1 = 5/10 = 0.5
r = term3/term2 = 2.5/5 = 0.5
r = term4/term3 = 1.25/2.5 = 0.5

We get the same common ratio (r = 1/2 = 0.5) each time, which helps confirm that we do indeed have a geometric sequence.
If r differed at all in any of the results above, then the sequence of course wouldn't be geometric.

Notice that -1 < r < 1 is the case.
r = 1/2 = 0.5 is between -1 and 1
This is sufficient criteria to confirm that the infinite geometric series converges to some value.
Having r in this range means we are adding smaller pieces to the partial sums to slowly approach some finite value.
Consider the case that r > 1. Such that r = 2 for instance. It should be fairly obvious the geometric sequence terms grow forever out of control. There's no way to approach a finite value.

Anyways, because r = 1/2 = 0.5, this means -1 < r < 1 is true. Therefore, the infinite geometric series converges

We can stop here since we've concluded the answer is choice D

This of course rules out choice A) diverges because that is the complete opposite of converging.

Choice B is ruled out as well. It is impossible for a geometric series to BOTH converge and diverge.
That would be like saying a door is fully closed and completely open at the same time.
This allows us to rule out choice B. Choice C is a similar story.

-------------------------------------------------

Extra stuff to consider. This section is optional.

If you are curious what the series converges to, then,
a = first term = 10
r = common ratio = 1/2 = 0.5
S = sum of the infinitely many geometric terms
S = a/(1-r)
S = 10/(1-0.5)
S = 10/0.5
S = 20

So if you were to add 10+5+2.5+1.25+... and go on forever doing this, then you'll land on 20.

Partial sums:
S2 = 10+5 = 15 = sum of the first two terms
S3 = 10+5+2.5 = 17.5 = sum of the first three terms
S4 = 10+5+2.5+1.25 = 18.75 = sum of the first four terms
S5 = 10+5+2.5+1.25+0.625 = 19.375 = sum of the first five terms
and so on...

Even when we get to something like S100, the sum of the first 100 terms, we'll never actually hit 20 itself. We'll get very close to it however.

As you can probably guess, there's a nice recursive nature going on.
That relationship is

Two examples:
S3 = S2 + a3
S3 = 15 + 2.5
S3 = 17.5
and
S4 = S3 + a4
S4 = 18.75 + 0.625
S4 = 19.375
This trick allows us to compute S5, S6, ... without having to write out long strings of summations.
Simply add on the newest term to the previous partial sum.
The drawback though is that if we wanted to compute S100 this way, we'd have to know what S99 was. Then in turn we'd have to know S98, and S97, and so on.

Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

The common ratio is 5/10 = 1/2.

An infinite geometric series converges if (and only if) the ratio r satisfies -1 < r < 1.

Is 1/2 between -1 and 1?

Question 1194660: Simplify and represent the following expression as a power of 2:
( 4 )^1 / 2 ( 8 )^1 / 3 ( 64 )^1 / 3
Select one:
a.
2 ^4

b.
2 ^3

c.
2 ^5

d.
2 ^2

If y = 2 x , then y 2 = _____.
Select one:
a.
2 2x

b.
a = - 3, n = - 2

c.
y / 2

d.
2 4x
Found 2 solutions by greenestamps, Alan3354:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

;
;
;

ANSWER: a. 2^4

In your second problem, I don't know what "y 2" in the statement of the problem means, nor do I know what "2 2x" and "2 4x" means in answer choices a and d.

If it means y squared, then use the standard notation "y^2"; if it means y^2, then the answer is (2x)^2 = 4x^2, which is none of the answer choices.

Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website!
Not clear.

Question 1194657: Given a triangle ABC, if A is 11 degrees, B is 49 degrees, and b is 45 cm, what is the length of a (round to one decimal.)
-----------------------------------------------------
What is the measure in degrees of the angle A = 7π / 6 radians?

Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website!
Given a triangle ABC, if A is 11 degrees, B is 49 degrees, and b is 45 cm, what is the length of a (round to one decimal.)
---------------
Use the Law of Sines:
a/sin(A) = b/sin(B)
a = 45*sin(11)/sin(49)
a = 11.4
=================================
What is the measure in degrees of the angle A = 7π / 6 radians?
Degs = (180/pi)*radians
(7pi/6)*(180/pi) = 210 degs

Question 1194645: Find the sum of the first 50 even positive integers.
Select one:
a.
2,550

b.
2,650

c.
2,600

d.
2,500
Found 2 solutions by Alan3354, math_tutor2020:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website!
Find the sum of the first 50 even positive integers.
-----------
Make 25 pairs:
2 + 100
4 + 98
6 + 96
etc
---> 102*25 = 2550

Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!

A = Set of first 50 positive even integers
A = {2, 4, 6, ..., 98, 100}
A = {2*1, 2*2, 2*3, ..., 2*49, 2*50}

Adding those items gets us this expression:
2*1+2*2+2*3+...+2*49+2*50
2*(1+2+3+...+49+50)

From here we need to calculate the sum of the first 50 positive integers

S = sum of the first n positive integers
S = n*(n+1)/2
S = 50*(50+1)/2
S = 50*51/2
S = 25*51
S = 1275
which point us to
1+2+3+...+49+50 = 1275

Therefore,
2*(1+2+3+...+49+50) = 2*1275 = 2,550

Answer: Choice A) 2,550

Question 1192691: 8/10 on the numberline
Found 2 solutions by josgarithmetic, Alan3354:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!
So draw the number line and plot the point. 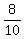is between 0 and 1, and nearer to 1 than to 0. Put it exactly where it needs to be.

Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website!
8/10 on the numberline
-------------
What's your question?

Question 1191660: Let f (x) =3x+2 and let g (x) square root of x-1. Find g (f(5))
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!

Therefore,