Question 1194661: What is the probabilty of getting a sum of 9 from two throws of dice?
Select one:
a.
1 / 3
b.
1 / 6
c.
1 / 9
d.
1 / 4
Found 3 solutions by MathLover1, ikleyn, greenestamps:
Answer by MathLover1(20849)   (Show Source):
You can put this solution on YOUR website!
When two dice are rolled together then total outcomes are  and
Sample space is
[ (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6)
(2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)
(3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6)
(4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)
(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)
(6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) ]
So, pairs with sum  are ( , ) ( ,  ) (, ) ( , ) i.e. total pairs
Total outcomes =
Favorable outcomes =
Probability of getting the sum of 9 = Favorable outcomes / Total outcomes
= 
So, P(sum of ) = .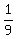
answer:
c.
Answer by ikleyn(52776)  (Show Source):
You can put this solution on YOUR website! .
On rolling dice problems see the lesson
- Rolling a pair of fair dice
in this site. You will find there many similar solved problems.
Read it and learn the subject from there. After that, you will be able easy solve such problems
ON YOUR OWN, which is your MAJOR GOAL visiting this forum (I believe).
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Solved problems on Probability".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
The solution from MathLover, as well as most of the examples on the link provided by tutor @ikleyn, solve the problem by looking at which outcomes in the sample space satisfy the given requirements. That is, of course, a valid way to solve a problem like this.
Another way to solve this kind of problem is to imagine rolling the two dice one at a time and considering the probability that each roll still makes it possible to get the desired end result.
For this problem, the sum of the two dice must be 9. Since the largest number on each die is 6, the outcome on the first die must be at least 3. The probability of that happening (die shows 3, 4, 5, or 6) is 4/6 = 2/3.
Then, once the first die has been rolled, for each number on the first die there is only 1 number on the second die that will give a sum of 9; so the probability of a "good" roll on the second die is 1/6.
Then the probability of a sum of 9 is the product of the probabilities of "good" outcomes on the rolls of both dice: (2/3)*(1/6) = 2/18 = 1/9.
|
|
|
