2x + y + 2z = 10
x + 2y + z = 8
3x + y - z = 2
Swap Rows 1 and 2 because a 1 is easier
to work with in the upper left corner
than a 2:
Get a 0 where the 2 is in Row 2
Multiply Row 1 by -2
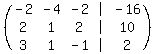Add Row 1 to row 2
Restore Row 1
Get a 0 where the 3 is in Row 3
Multiply Row 1 by -3
Add Row 1 to Row 3
Restore Row 1
Get a 1 where the -3 is in Row 2
Multiply Row 2 through by -1/3, or
you can divide Row 2 by -3 (same thing)
Get a 0 where the -5 is
Multiply Row 2 by 5
Add Row 2 to row 3
Restore Row 2
Get a 1 where the -4 is
Multiply Row 3 by -1/4, or
Divide Row 3 by -4 (same thing)
Interpret as a new system of equations
in echelon (triangular) form:
1x + 2y + 1z = 8
0x + 1y + 0z = 2
0x + 0y + 1z = 3
or
x + 2y + z = 8
y = 2
z = 3
Then we see that z = 3 and y = 2
Substitute in the top equation:
x + 2(2) + 3 = 8
x + 4 + 3 = 8
x + 7 = 8
x = 1
Solution (x,y,z) = (1,2,3)
Edwin
