SOLUTION: how do i find the unit vectors in the same direction as U and V if U=(-3, 9 -3) and V=(4, -1, 7)

Algebra ->  Matrices-and-determiminant -> SOLUTION: how do i find the unit vectors in the same direction as U and V if U=(-3, 9 -3) and V=(4, -1, 7)       Log On


   

Question 391693: how do i find the unit vectors in the same direction as U and V if U=(-3, 9 -3) and V=(4, -1, 7)

Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
how do i find the unit vectors in the same direction as U and V if U=(-3, 9 -3) and V=(4, -1, 7)

Points are enclosed in parentheses and vectors are enclosed in <  > 
So I can't tell whether you mean this:

Find a unit vector in the same direction as vector UV whose
endpoints are the points U(-3,9, -3) and V(4, -1, 7)

or this:

Find a unit vector in the same direction as vector U = < -3, 9, -3 >
and find a unit vector is the same direction as vector V = < 4, -1, 7 > 

---------------------------------------

If you mean the first way, then

 UV = < 4-(-3), -1-9, 7-(-3) > = < 7, -10, 10 >

A unit vector in the same direction as UV would be found by
dividing each component by the "norm" (also called the absolute value or the
length of the vector).

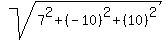sqrt%287%5E2%2B%28-10%29%5E2%2B%2810%29%5E2%29 = sqrt%28249%29

Then a unit vector in the direction of < 7, -10, 10 > is

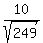< 7%2Fsqrt%28249%29, -10%2Fsqrt%28249%29, 10%2Fsqrt%28249%29 >

-------------------------------------

If you mean the second way, then

 U = < -3, 9, -3 > 

A unit vector in the same direction as U would be found by
dividing each component by the "norm" (also called the absolute value or the
length of the vector).

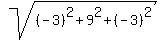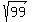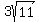sqrt%28%28-3%29%5E2%2B9%5E2%2B%28-3%29%5E2%29 = sqrt%2899%29 = 3sqrt%2811%29

Then a unit vector in the direction of < -3, 9, -3 > is

< -3%2F%283sqrt%2811%29%29, 9%2F%283sqrt%2811%29%29, -3%2F%283sqrt%2811%29%29 >

or

< -1%2F%28sqrt%2811%29%29, 3%2F%28sqrt%2811%29%29, -1%2F%28sqrt%2811%29%29 


and

 V = < 4, -1, 7 > 

A unit vector in the same direction as V would be found by
dividing each component by the "norm" (also called the absolute value or the
length of the vector).

sqrt%284%5E2%2B%28-1%29%5E2%2B7%5E2%29 = sqrt%2866%29 = sqrt%2866%29

Then a unit vector in the direction of < 4, -1, 7 > is

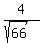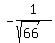< 4%2F%28sqrt%2866%29%29, -1%2F%28sqrt%2866%29%29, 7%2F%28sqrt%2866%29%29 >

-------------------------------------------------------------
Note: if you post in here and use this character " < " be sure to skip a space
after it because that character is used to introduce an HTML tag and if
you don't skip a space immediately afterward it will delete whatever is
after it.

Edwin