SOLUTION: find the product of 2 3 5 0 1 2 x 4 2 -1 0 -3 2

Algebra ->  Matrices-and-determiminant -> SOLUTION: find the product of 2 3 5 0 1 2 x 4 2 -1 0 -3 2       Log On


   

Question 347423: find the product of
2 3 5
0 1 2

x
4 2
-1 0
-3 2
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
See this solver for more help with multiplying matrices.

Since the first matrix is a 2 by 3 matrix and the second matrix is a 3 by 2 matrix, this means that the resulting matrix will be a 2 by 2 matrix. The final matrix will have the same number of rows as the first matrix and the same number of columns as the second matrix.

So the final resulting matrix will look like:


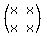
%28matrix%282%2C2%2Cx%2Cx%2Cx%2Cx%29%29


note: the "x"s are just placeholders for now



--------------------------------------------------




Multiply the corresponding entries from the 1st row of the first matrix by the 1st column of the second matrix. After multiplying, add the values:


1st row, 1st column:
%282%29%2A%284%29%2B%283%29%2A%28-1%29%2B%285%29%2A%28-3%29=8%2B-3%2B-15=-10


So the element in the 1st row, 1st column of the resulting matrix is -10. Now let's update the matrix:

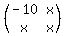
%28matrix%282%2C2%2C-10%2Cx%2Cx%2Cx%29%29
--------------------------------------------------




Multiply the corresponding entries from the 1st row of the first matrix by the 2nd column of the second matrix. After multiplying, add the values:


1st row, 2nd column:
%282%29%2A%282%29%2B%283%29%2A%280%29%2B%285%29%2A%282%29=4%2B0%2B10=14


So the element in the 1st row, 2nd column of the resulting matrix is 14. Now let's update the matrix:

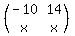
%28matrix%282%2C2%2C-10%2C14%2Cx%2Cx%29%29




================================================================================




Multiply the corresponding entries from the 2nd row of the first matrix by the 1st column of the second matrix. After multiplying, add the values:


2nd row, 1st column:
%280%29%2A%284%29%2B%281%29%2A%28-1%29%2B%282%29%2A%28-3%29=0%2B-1%2B-6=-7


So the element in the 2nd row, 1st column of the resulting matrix is -7. Now let's update the matrix:

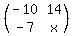
%28matrix%282%2C2%2C-10%2C14%2C-7%2Cx%29%29
--------------------------------------------------




Multiply the corresponding entries from the 2nd row of the first matrix by the 2nd column of the second matrix. After multiplying, add the values:


2nd row, 2nd column:
%280%29%2A%282%29%2B%281%29%2A%280%29%2B%282%29%2A%282%29=0%2B0%2B4=4


So the element in the 2nd row, 2nd column of the resulting matrix is 4. Now let's update the matrix:

%28matrix%282%2C2%2C-10%2C14%2C-7%2C4%29%29








==============================================================================


Answer:


So the solution is %28matrix%282%2C2%2C-10%2C14%2C-7%2C4%29%29

In other words,



Once again, see this solver for more help with multiplying matrices.