SOLUTION: Combine methods of row reduction and cofactor expansion to calculate determinants. -1 2 3 0 3 4 3 0 5 4 6 6 4 2 4 3

The 4th column already has 2 zeros,
and we need to get one more zero in
it.

So we will multiply the 4th row by
-2 and add it to the 3rd row, and
then restore the 4th row

4th row = 



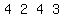multiply it by -2:



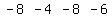add that to the third row:



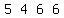and get



Replace the 3rd row by that and keep
the 4th as it was:



Now the only non-zero element in the
4th column is the 3 in the bottom
right hand corner. Its minor consists
of the 3x3 determinant of all the
elements which are NOT in either
the same row or the same column as
the cofactor 3, that is, this 3x3
determinant:

 

Next we multiply the cofactor 3 by
this determinant:

 

But we have to determine whether to
multiply this product by +1 or -1 by 
this "checkerboard" scheme of alternating
"+1"'s and "-1"'s:



The cofactor was in the position of
the 4th row 4th column, the bottom
right hand corner, and we see
that has "+1" in it so we multiply
the product by "+1" and get what we had.

 

 Now we work on the 3x3 determinant.
the 2nd column already has one zero,
so we can get a zero where the 4 is
by multiplying the 1st row by -2 and
adding it to the 2nd row and then
restoring the 1st row:

The 1st row is 



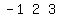we multiply it by -2, getting



and add that to row 2, which is

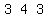, and get

.

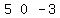Then we replace the 2nd row by that,
and leave the 1st row as it was,
getting:

 

We see that the only non-zero element 
in the 2nd column is the 2 in the middle
of the top row. Its minor consists
of the 2x2 determinant of all the
elements which are NOT in either
the same row or the same column as
the cofactor 2, that is, this 2x2
determinant:

 

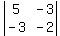Next we multiply the cofactor 2 by
this determinant, retaining the 3
multiplier we already had:

 

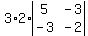But we have to, as before, determine 
whether to multiply this product by
+1 or -1 by this "checkerboard" scheme 
of alternating "+1"'s and "-1"'s:



This time the cofactor was in the same
position as the "-1" in the middle of
the top row, so we must multiply by -1,
and get:

  

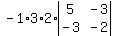Now we could take this 2x2 determinant
down to a 1x1 determinant, but we don't
bother, and just use the difference of
the diagonal products, so we have







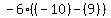
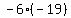
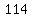Edwin