SOLUTION: Hi. I am trying to make a determinant problem for someone I am tutoring. I would like something similar to the following problem that requires factoring in the result, the answer t

Here's how to make as many of them as you like.  

1. Choose any integer that you want to be one of
the values of x, the solution to the problem.

I'll arbitrarily choose x=2

2. Choose any two multiples of that number, positive or negative. 

I'll choose two arbitrary multiples of 2, as 6 and 8.

3. Make up any determinant that contains those two multiples such
that neither is in the same row or column as the other.  Evaluate 
the determinant.

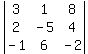 = 14

Notice I put the 6 in the 3rd row 2nd column position
and the 8 in the 1st row 3rd column position, and I
evaluated the determinant as 14.

Since x=2, now all I have to do is replace the 6 by 2x and 
the 8 by 4x

 = 14

If you evaluate the determinant you get:



Divide through by 8



So there are two solutions,

 and 

You can even have more fun with that determinant because 
it has a 4 and a -2.  The 4 is 2x and the -2 is -x.
So you can replace them too.  Like this: 

 = 14

However make sure you don't have x's so as to give a 
third degree equation. Always leave one row or column 
without any unknowns. I chose to leave the first column 
without unknowns,  Notice if had put an x where the
2 is in the 2nd row 1st column, it would have resulted in
a cubic equation.

But as it is, the equation comes out




So there are two solutions here,  and    

It's interesting that even though  was the same in
both problems, the other solution was not the same as the
other solution in the first problem. 

Edwin