|
Question 19634: My question is.... I was wondering how to do the cramer rule on a 3x3. I have found a bunch of examples and stuff, but I want to know how in the world do you find the determinants of the D, Dx, Dy.and Dz. If you could just tell me how, that would be great.
Answer by venugopalramana(3286)   (Show Source): (Show Source):
You can put this solution on YOUR website! SEE THE FOLLOWING AND COME BACK IF YOU HAVE DIFFICULTY.HERE C,CX,CY,CZ REFER TO YOUR D,DX,DY,DZ...JUST A DIFFERENCE IN NOMENCLATURE.I SHOWED IN DETAIL A 2X2 DETERMINANT AND THEN IN BRIEF A 3X3 DETERMINANT
2x+y=4
3x-y=6
make a deteminant with coefficients of x (2,3)and y(1,-1) in the 2 eqns.call it C.(Actually for a determinant as you know ,the numbers are contained in vertical bars at either end like |xx|,but in the following the bars are omitted due to difficulty in depiction.you may assume the bars are present)
C=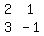 =2*(-1)-(1*3)=-5 =2*(-1)-(1*3)=-5
..now use the constants (4,6)to replace coefficients of x(2,3) in the above determinant C...call it CX..
CX= =4*(-1)-1*6=-4-6=-10 =4*(-1)-1*6=-4-6=-10
..now use the constants (4,6)to replace coefficients of y(1,-1) in the above determinant C...call it CY..
CY= =2*6-3*4=12=12=0 =2*6-3*4=12=12=0
..now cramers rule says that
 ..so we get ..so we get
x/(-10)=y/0=1/-5
x=-10/-5=10/5=2
y=0/-5=0
************************************
so using the above method you can do the next problem ..here due to presence of 3 variables you will get 3rd.order determinants...4 in all...namely C,CX,CY and CZ,the last formula also extends to include z ,
 .. ..
but the procedure is same ..
2x+3y+ z= 5
x+y-2z= -2
-3x +z=-7 ...
...just to give you the idea
C= ..and ..and
CZ= ..etc..hope you can work out the rest ..etc..hope you can work out the rest
|
|
|
| |