|
Question 17820: Please help I have no idea how to do this problem: Use Cramer's Rule to solve each system.
1. 2x+y=4
3x-y=6
2. 2x+3y+ z= 5
x+y-2z= -2
-3x +z=-7
Answer by venugopalramana(3286)   (Show Source): (Show Source):
You can put this solution on YOUR website! 2x+y=4
3x-y=6
make a deteminant with coefficients of x (2,3)and y(1,-1) in the 2 eqns.call it C.(Actually for a determinant as you know ,the numbers are contained in vertical bars at either end like |xx|,but in the following the bars are omitted due to difficulty in depiction.you may assume the bars are present)
C=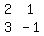 =2*(-1)-(1*3)=-5 =2*(-1)-(1*3)=-5
..now use the constants (4,6)to replace coefficients of x(2,3) in the above determinant C...call it CX..
CX= =4*(-1)-1*6=-4-6=-10 =4*(-1)-1*6=-4-6=-10
..now use the constants (4,6)to replace coefficients of y(1,-1) in the above determinant C...call it CY..
CY= =2*6-3*4=12=12=0 =2*6-3*4=12=12=0
..now cramers rule says that
 ..so we get ..so we get
x/(-10)=y/0=1/-5
x=-10/-5=10/5=2
y=0/-5=0
************************************
so using the above method you can do the next problem ..here due to presence of 3 variables you will get 3rd.order determinants...4 in all...namely C,CX,CY and CZ,the last formula also extends to include z ,
 .. ..
but the procedure is same ..
2x+3y+ z= 5
x+y-2z= -2
-3x +z=-7 ...
...just to give you the idea
C= ..and ..and
CZ= ..etc..hope you can work out the rest ..etc..hope you can work out the rest
|
|
|
| |