SOLUTION: How do I find B-CF? B= [2,8,.6,3] C=[12,0,1.5,1,-6,7] F=[-2,0,0,8,2,1]

Algebra ->  Matrices-and-determiminant -> SOLUTION: How do I find B-CF? B= [2,8,.6,3] C=[12,0,1.5,1,-6,7] F=[-2,0,0,8,2,1]      Log On


   

Question 175431: How do I find B-CF?
B= [2,8,.6,3] C=[12,0,1.5,1,-6,7] F=[-2,0,0,8,2,1]
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
I'm guessing on the make up of the matrices.
First off let's look at [C][F].
[C]=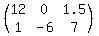%28matrix%282%2C3%2C12%2C0%2C1.5%2C1%2C-6%2C7%29%29
[F]=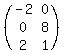%28matrix%283%2C2%2C-2%2C0%2C0%2C8%2C2%2C1%29%29
[C][F]=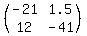%28matrix%282%2C2%2C-21%2C1.5%2C12%2C-41%29%29
where each element of [C][F] comes from multiplying a row of [C] with a column of [F].
Example: First element is product of first row and first column.
CF%5B1%2C1%5D=12%2A-2%2B0%2A0%2B1.5%2A2=-24%2B3=-21
.
.
.
Now that we have [C][F], we can subtract it from [B], element by element,
[B]-[C][F]=%28matrix%282%2C2%2C2%2C8%2C.6%2C3%29%29-%28matrix%282%2C2%2C-21%2C1.5%2C12%2C-41%29%29
[B]-[C][F]=%28matrix%282%2C2%2C23%2C6.5%2C-11.4%2C44%29%29
.
.
.
If this is not how the matrices look,please re-state the problem and be more specific about the make up of the matrices (rows x columns).
Here's an example.
[A] is a 2x2 matrix. A=[1,2,3,4].
The assumption is that [A] looks like this,
[A]=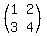%28matrix%282%2C2%2C1%2C2%2C3%2C4%29%29
[B] is a 3x2 matrix. B=[5,6,7,8,9,10]
[B]=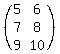%28matrix%283%2C2%2C5%2C6%2C7%2C8%2C9%2C10%29%29