SOLUTION: <pre><b> what is the value of this determinant? {{{abs(matrix(6,6, 1, 1, 1, 1, 1, 1, 0, 1, 0, -1, 0, -1, 1, 2, 0, 3, 2, 0, 1, 0, 3, 2, 0,

what is the value of this determinant?

                             thank you!

The third column has the most 0's, so
we'll expand about it after we make it
have all 0's but one.

Let's make the 3 in the 3rd column a 0
by adding -3 times the 1st row to 1
times the 4th row:





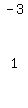
Now we expand this 6x6 matrix by
the 3rd column.  Since there is only
1 non-zero element in the 3rd column,
the 1 at the top.  We notice that it
is in row 1 and column 3, so we add
1+3 and get 4, and 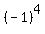=+1 we
multiply the 1 in the top row by +1
and so the determinant is +1 times the
5x5 determinant formed by removing
both row 1 and column 3:



The first row has the most 0's, so
we'll expand about it after we make it
have all 0's but one.

Let's make the -1 in the 1st row 3rd 
column a 0 by adding 1 times the 2nd 
column to 1 times the 3rd column:

     1   1




Let's make the -1 in the 1st row 5th 
column a 0 by adding 1 times the 2nd 
column to 1 times the 5th column:

     1          1 




Now we expand this 5x5 matrix by
the 1st row.  Since there is only
1 non-zero element in the 1st row,
the 1 at the 1st row 2nd column.
Since it is in row 1 and column 2, so we add
1+2 and get 3, and =-1 we
multiply the 1 in the top row by -1
and so the determinant is -1 times the
4x4 determinant formed by removing
both row 1 and column 2:



We can simplify by multiplying the -1
by the 2nd row, changing their signs
to positive:



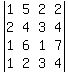Unfortunately there are no 0's at
all.  So we'll make some.  The
simplest row or column is the 1st
column.  To make the 2 in the
1st column a 0, add -2 times the
1st row to 1 times the 2nd row:




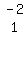
Now since that 0 popped up
over there in the second row,
that makes us change plans, for
now we have 2 0's in the 2nd row.

So we change plans and now we 
want to expand about the 2nd
row.  So we can get a 0 where
the -6 is by multiplying the
3rd column by -6 and adding it
to 1 times column 2.



Now we expand this 4x4 matrix by
the 2nd row.  Since there is only
1 non-zero element in the 1st row,
the -1 at the 2nd row 3rd column.
Since it is in row 2 and column 3, we add
2+3 and get 5, and 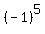=-1, we
multiply the -1 in the 2nd row 3rd column
by -1 and so the determinant is 1 times the
3x3 determinant formed by removing
both row 2 and column 3:



The
simplest row or column is the 2nd
row.  To make the 7 a 0, we add
-7 times the 1st column to 1 times 
the 3rd column:

-7   1




Now we expand this 3x3 matrix by
the 2nd row.  Since there is only
1 non-zero element in the 2nd row,
the 1 at the 2nd row 1st column.
Since it is in row 2 and column 1, we add
2+1 and get 3, and =-1, we
multiply the 1 in the 2nd row 1st column
by -1 and so the determinant is -1 times the
2x2 determinant formed by removing
both row 2 and column 1:



We can simplify by multiplying the -1
by the 1st row, which changing the signs:




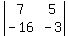To expand, it's just the difference of
the product of the upper left to lower
right diagonal and the product of the
upper right to lower left diagonal.

(7)(-3)-(5)(-16)=-21+80=59

So the value of the determinant is 59.

Edwin