|
Question 14571: Help me please!
I don't understand what I am suppose to do.
Evaluate the determinant of the matrix.
items in a bracket. 3 -2 0
-1 5 3
2 7 1
Found 3 solutions by glabow, dolphingurl, venugopalramana:
Answer by glabow(165)   (Show Source): (Show Source):
You can put this solution on YOUR website! The underlying meaning of a determinant is complex and cannot be covered here. It is a useful value to know when working with matrices. There are a couple of ways of calculating the determinant of a matrix, and for a 3 x 3 there is a relatively easy procedure. I'm surpised you haven't been given it (if you haven't) but I'll try it here.
You first get the products of all the left-to-right diagonals of the matrix and add them up. You then get the products of all the right-to-left diagonals of the matrix and add them up. You then subtract the right-to-left sum from the left-to-right sum. The diagonals are all referenced from top to bottom.
You can see how this is a very poor way to describe the procedure. Let's make it mathematical.
We will reference the elements of the matrix with the following notation:
 will mean the element in row x and column y. will mean the element in row x and column y.
In a 3 x 3 matrix the upper left element will be 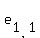 and the lower right element will be and the lower right element will be 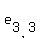 . Get it? . Get it?
Okay. The left-to-right diagonals are as follows:
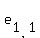 , ,  , , 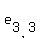 ; ;  , , 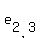 , , 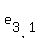 ; and ; and  , , 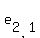 , , 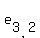
Whew! For the matix values you gave, this amounts to
(3 x 5 x 1), (-2 x 3 x 2), and (0 x -1 x 7). Do the multiplications and add them up.
15+(-12)+0 = 3. This is the value of the products of all the left-to-right diagonals.
The right-to-left diagonals are as follows:
 , ,  , , 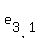 ; ;  , , 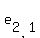 , , 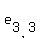 ; and ; and 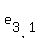 , , 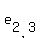 , , 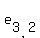
For the matrix values you gave, this amounts to
(0 x 5 x 2), (-2 x -1 x 1), and (3 x 3 x 7). Do the multiplications and add them up.
0+2+63 = 65. This is the value of the products of all the right-to-left diagonals.
Subtract the right-to-left from the left-to-right.
Determinant = 3 - 65 = -62
CHECK MY WORK!!!
Answer by dolphingurl(4)   (Show Source): (Show Source):
You can put this solution on YOUR website! Well,the underlying meaning of a determinant is complex and cannot be covered here. It is a useful value to know when working with matrices. There are a couple of ways of calculating the determinant of a matrix, and for a 3 x 3 there is a relatively easy procedure. I'm surpised you haven't been given it (if you haven't) but I'll try it here.
You first get the products of all the left-to-right diagonals of the matrix and add them up. You then get the products of all the right-to-left diagonals of the matrix and add them up. You then subtract the right-to-left sum from the left-to-right sum. The diagonals are all referenced from top to bottom.
You can see how this is a very poor way to describe the procedure. Let's make it mathematical.
We will reference the elements of the matrix with the following notation:
will mean the element in row x and column y.
In a 3 x 3 matrix the upper left element will be and the lower right element will be . Get it?
Okay. The left-to-right diagonals are as follows:
, , ; , , ; and , ,
Whew! For the matix values you gave, this amounts to
(3 x 5 x 1), (-2 x 3 x 2), and (0 x -1 x 7). Do the multiplications and add them up.
15+(-12)+0 = 3. This is the value of the products of all the left-to-right diagonals.
The right-to-left diagonals are as follows:
, , ; , , ; and , ,
For the matrix values you gave, this amounts to
(0 x 5 x 2), (-2 x -1 x 1), and (3 x 3 x 7). Do the multiplications and add them up.
0+2+63 = 65. This is the value of the products of all the right-to-left diagonals.
Subtract the right-to-left from the left-to-right.
Determinant = 3 - 65 = -62.
And that will be your answer. Does that help you understand what to do?
Answer by venugopalramana(3286)   (Show Source): (Show Source):
You can put this solution on YOUR website! Help me please!
I don't understand what I am suppose to do.
Evaluate the determinant of the matrix.
items in a bracket. 3 -2 0
-1 5 3
2 7 1
The determinant of matrix

is evaluated in the usual manner as that of a determinant.IF IT IS NOT KNOWN TO YOU IT CAN BE EXPLAINED ON HEARING FROM YOU>
taking any one column or row .Expanding by using the first column of 3,-1,2 we get the value of the determinant as
=3*(5*1-3*7)-(-1)*((-2)*1-0*7)+2*((-2)*3-0*5)
=-48-2-12=-62
|
|
|
| |