|
Question 1207232: A volleyball team is playing in a tournament. The probability that they will win their first match is 60%. The coach noticed that when the team wins a match, the probability that they will win the next match rises to 80%. If they lose a match, the probability that they will win the next match falls to 25%.
a) Write the initial probability matrix and the transition matrix.
b) Determine the probability that the team will win its third match.
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
Let's for a moment do this without use of Markov notation and matrices.
The next section will handle that. You can skip directly to that section if you prefer.
Events
W1 = win 1st match
W2 = win 2nd match
W3 = win 3rd match
L1 = lose 1st match
L2 = lose 2nd match
L3 = lose 3rd match
For the first match
P(W1) = 0.60
P(L1) = 0.40
If the team wins the first match,
P(W2 given W1) = 0.80
P(L2 given W1) = 0.20
The "given" refers to conditional probability.
You can use a vertical bar to represent the key term "given", but I prefer to use the word to avoid potential confusion with the number one or lowercase L.
If the team loses the first match,
P(W2 given L1) = 0.25
P(L2 given L1) = 0.75
Use the Law of Total Probability to get:
P(W2) = P(W2 and W1) + P(W2 and L1)
P(W2) = P(W2 given W1)*P(W1) + P(W2 given L1)*P(L1)
P(W2) = 0.80*0.60 + 0.25*0.40
P(W2) = 0.48 + 0.10
P(W2) = 0.58
which immediately gives us P(L2) = 1-P(W2) = 1-0.58 = 0.42
A probability tree diagram might be helpful.
The numbers at the very bottom represent multiplications along that specific branch.
Example: 0.60*0.80 = 0.48 along the left-most pathway
Notice P(W2) = P(W2 and W1) + P(W2 and L1) = 0.48+0.10 = 0.58
We have:
P(W2) = 0.58
P(L2) = 0.42
If the team wins the second match,
P(W3 given W2) = 0.80
P(L3 given W2) = 0.20
If the team loses the second match,
P(W3 given L2) = 0.25
P(L3 given L2) = 0.75
Apply the Law of Total Probability once again:
P(W3) = P(W3 and W2) + P(W3 and L2)
P(W3) = P(W3 given W2)*P(W2) + P(W3 given L2)*P(L2)
P(W3) = 0.80*0.58 + 0.25*0.42
P(W3) = 0.569 is probability the team wins the 3rd match.
Once again, a probability tree diagram might help visualize what's going on here.
This is what the template will look like
I'll let the student fill it out.
------------------------------------------------------------------------------------------------------------------------------------
Now we'll apply Markov mathematics.
Your teacher presented you with 3 facts- Fact 1: The probability that they will win their first match is 60%
- Fact 2: When the team wins a match, the probability that they will win the next match rises to 80%.
- Fact 3: If they lose a match, the probability that they will win the next match falls to 25%.
W = win
L = lose
Draw two circles. Label one of them W and the other L.
From circle W, draw an arrow that will point back to W. It loops around.
Label this arrow as 0.80
It represents the idea that if we start with a win, then the probability of another win is 80%. See fact 2 above.
From circle W draw an arrow that points to L. This arrow is labeled 0.20
From circle L draw arrows that point to itself and to W; they will be labeled 0.25 and 0.75 respectively. These labels are due to fact 3.
Here is the arrow diagram
Such a diagram is optional, but may be helpful.
Now we'll build the transition matrix.
The rows will represent the initial state and the columns the final state.
I like to think of it as reading from left to right "start --> finish".
We'll start with a certain row and end up at a certain column.
Here's what the blank template looks like
And here's what happens when filling out the transition matrix.
Example: row1 --> column2 represents going from a win to a loss, of which has probability 0.20 = 20%
Label this as matrix T.
Adding along any given row results in a sum of 1.
The initial probability matrix is going to consist of 1 row and 2 columns.
The 1 row represents the initial state, which doesn't have a win or loss tag to it yet.
The 2 columns represent the final state after that 1st match either W or L.
The initial probability matrix is  which should be fairly self explanatory. See fact 1.
Computing  will lead to  which matches what we got in the first section above (when we arrived at P(W2) = 0.58 and P(L2) = 0.42)
I'll leave the matrix multiplication scratch work for the student to do.
Once we determine matrix PT, we will then apply another multiplication with the transition matrix T to compute PT*T = PT^2
This will determine the probability values for the 3rd match.
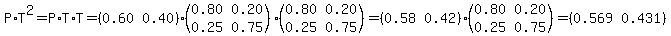
This aligns with what we got in the first section above.
------------------------------------------------------------------------------------------------------------------------------------
Answers:
(a) Initial probability matrix is and transition matrix is
P is a 1x2 matrix while T is a 2x2 matrix.
(b) The probability the team wins its third match is 0.569 = 56.9%
|
|
|
| |
