|
Question 1205477: I don't know how to format matrices on here, so I will write the top row (horizontal) first and then the bottom row.
Consider the following matrices:
A = [4, -1][-6, -3]
B = XA, where X is the 2x2 matrix that dilates vectors by a factor of 2
C = The 3x3 matrix that reflects vectors across the plane x + y + z = 1
D = [4, -1, 5][0, -3, -3][0, 0, -5]
Calculate the four absolute values |det(A)|, |det(B)|, |det(C)|, and |det(D)|.
Answer by ikleyn(52832)   (Show Source):
You can put this solution on YOUR website! .
I don't know how to format matrices on here, so I will write the top row (horizontal) first and then the bottom row.
Consider the following matrices:
A = [4, -1][-6, -3]
B = XA, where X is the 2x2 matrix that dilates vectors by a factor of 2
C = The 3x3 matrix that reflects vectors across the plane x + y + z = 1
D = [4, -1, 5][0, -3, -3][0, 0, -5]
Calculate the four absolute values |det(A)|, |det(B)|, |det(C)|, and |det(D)|.
~~~~~~~~~~~~~~~~~~~~~~~
(a) Matrix A is
A =  .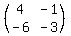
Its determinant is det(A) = 4*(-3) - (-6)*(-1) = -12 - 6 = -18.
The absolute value of the determinant A is |det(A)| = |-18| = 18.
Usually, at normal pedagogic process, a student learns the notion/(the conception)
of a matrix and its determinant and how to calculate it in the same day
(from the same lecture of a professor or from a textbook).
(b) Matrix X, which is 2x2 matrix that dilates vecors by a factor of 2 is the diagonal matrix
X = 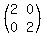 with the scalar elements of 2 in its diagonal.
Multiplication by matrix X from the left (XA) acts on matrix A by multiplying all elements of A
by the scalar of 2. So, the product XA is
XA =  .
You can calculate XA directly by making direct multiplication, or you can restore the product XA
using the rule above.
Next, if the rows of the matrix are multiplied by 2, then, according to the rules of determinant,
det(XA) is equal to det(A) multiplied by 2*2 = 4.
Using this property of determinants, you can get det(XA) = 4*det(A) = 4*(-18) = -72 and
|det(XA)| = |-72| = 72.
Alternatively, you can calculate det(XA) directly, based on the formal rule of calculating determinants.
Surely, you will get the same value.
(c) Determinant of this reflection matrix can be found without calculations,
and even without writing of this matrix in explicit form.
Determinant of this matrix is +/-1, since this geometric operation of reflection conserves the volume.
Therefore, the absolute value of the determinant of this matrix is |det(C)| = 1.
(d) Matrix D is an upper triangular matrix.
The determinant of such matrix is the product of its diagonal elements det(D) = 4*(-3)*(-5) = 4*15 = 60.
Therefore, |det(D)| = |60| = 60.
Solved. I answered all your questions.
////////////////////
Level of question (a) is 0 (zero): a student should know it from the professor lecture or from a textbook
in the first day as the matrices and determinants are explained and introduced.
Level of question (b) is between 0.5 and 1, which means that from one half of
the thought to one whole thought is needed
Level of question (c) is between 2 and 2.5, which means that you may learn it either from an
advanced professor lecture or from an advanced textbook.
Level of question (d) is 1, which means that almost everybody should know the answer and the method,
but usually it is learned not at the first day, but somewhen later.
|
|
|
| |
