.
.
FOUR MEN AND 8 WOMEN CAN FINISH A PIECE OF WORK JOINTLY IN 5 DAYS WHILE 3 MEN AND 2
WOMEN CAN FINISH THE SAME WORK JOINTLY IN 10 DAYS. FIND THE TIME TAKEN BY ONE MAN
ALONE AND THAT OF ONE WOMAN ALONE TO FINISH THE SAME WORK.
~~~~~~~~~~~~~~~
Let m be the rate of work of one man and let w be the rate of work of one woman.
Then we have this system of 2 equations in 2 unknowns
4m + 8w =  (1)
3m + 2w =
(1)
3m + 2w =  (2)
To run of the denominator, I will multiply eq(1) by 5 (both sides) and will multiply eq(2) by 20.
I will get then
20m + 40w = 1 (3)
60m + 40w = 2 (4)
Next, I will subtract eq(3) from eq(2). I will get
40m = 1, hence m =
(2)
To run of the denominator, I will multiply eq(1) by 5 (both sides) and will multiply eq(2) by 20.
I will get then
20m + 40w = 1 (3)
60m + 40w = 2 (4)
Next, I will subtract eq(3) from eq(2). I will get
40m = 1, hence m =  .
Now from eq((3),
.
Now from eq((3),
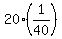 + 40w = 1,
which gives then
40w = 1 -
+ 40w = 1,
which gives then
40w = 1 -  =
=  , w =
, w = 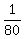 .
The problem is just solved: a single man will do the job in 40 days, working alone;
a single woman will do it in 80 days.
.
The problem is just solved: a single man will do the job in 40 days, working alone;
a single woman will do it in 80 days.
Solved.