Question 1153918: The graph of a parabola passes through the points (3/2, 4/3) and (0, −6) and
has a horizontal tangent line at (3/2, 4/3). Find an equation for the parabola
and sketch its graph.
Answer by ikleyn(52792)   (Show Source):
You can put this solution on YOUR website! .
Since the parabola has a horizontal tangent line at the point (3/2,4/3), it means
that this point (3/2,4/3) is the vertex of the parabola.
Hence, the parabola has the form
y(x) =  ,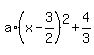
where "a" is a coefficient (real number), now unknown.
To find "a", use the fact that the plot of the parabola passes through the point (0,-6). It means that
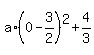y(0) = -6, or  = -6, or
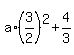 = -6.
It gives
 =  =  =  ,
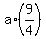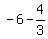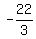hence
a =  =  .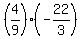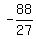
Thus the equation of the parabola is
y(x) =  .
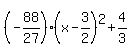You can transform it to any other equivalent form you wish.
Regarding the plot, do it on your own.
You may use free of charge plotting tools from the Internet.
|
|
|
