|
Tutors Answer Your Questions about Linear-equations (FREE)
Question 1207383: The equation 5/(x + 3) + 3 = (8 + x)/(x + 3) has no solution, yet when we go through the process of solving it we obtain x = -3. Why is that the case?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The value x = -3 is PROXIBITED for this equation,
since the fractions in both sides of this equations are not defined at x = -3.
As people say in Math, the value x = -3 is not in the domain of this equation,
while we are looking for the solutions that ARE in the domain.
When we get the solution x = -3, we get it for ANOTHER, transformed equation,
and this value does not work for the original equation.
The original equation and the transformed equation are NOT equivalent.
This is a complete explanation, in few words. Full and complete.
Question 1210353: What's 3 and a third * 5/9?
Found 2 solutions by AnlytcPhil, MathLover1:
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1210283: A company’s revenue is modeled by 𝑅(𝑥) = 50𝑥 −200, where x is the number of units sold.
1. Graph 𝑅(𝑥). Label the axes in context. Show the
scale used for both the x- and y-axis.
2. Find R(0) and interpret this value in context.
3. Determine how many units must be sold for
revenue to break even (𝑅(𝑥)=0).
answer: 1. x-intercept (0,-200) y-intercept (4,0)
2 R(0)= -200
3. [R(x) = 0]; X=4 (units to be sold)
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
.
1. Graph 𝑅(𝑥). Label the axes in context. Show the
scale used for both the x- and y-axis.
 2. Find R(0) and interpret this value in context.
The point R(0) = (0,-200) represents the fact that we start out $200 "in the
hole" because in the beginning we haven't sold any units (0 units sold).
3. Determine how many units must be sold for
revenue to break even (𝑅(𝑥)=0).
The "break-even" point is the x-intercept, when the revenue R(x) = 0.
We set R(x) = 0
R(x) = 50x-200 = 0
50x = 200
x = 4
So the break-even point is (4,0). It's when we've sold enough units to get us
"out of the hole", even though we haven't made a profit yet. To break-even, we
need to have sold 4 units.
answer: 1. x-intercept (0,-200) y-intercept (4,0)
2 R(0)= -200
3. [R(x) = 0]; X=4 (units to be sold)
Edwin
2. Find R(0) and interpret this value in context.
The point R(0) = (0,-200) represents the fact that we start out $200 "in the
hole" because in the beginning we haven't sold any units (0 units sold).
3. Determine how many units must be sold for
revenue to break even (𝑅(𝑥)=0).
The "break-even" point is the x-intercept, when the revenue R(x) = 0.
We set R(x) = 0
R(x) = 50x-200 = 0
50x = 200
x = 4
So the break-even point is (4,0). It's when we've sold enough units to get us
"out of the hole", even though we haven't made a profit yet. To break-even, we
need to have sold 4 units.
answer: 1. x-intercept (0,-200) y-intercept (4,0)
2 R(0)= -200
3. [R(x) = 0]; X=4 (units to be sold)
Edwin
Question 1210277: Equation of line (-2,6) and parallel to y=5x+12
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Parallel lines have the same slope.
The slope of the line with the given equation is 5; the slope of the parallel line will be 5.
The equation of the parallel line will be of the form y=5x+b.
To find the equation of the line parallel to the given line passing through the given point (x,y)=(-2,6), substitute those x and y values in the general equation and solve for b.
y = 5x+b
6 = 5(-2)+b
6 = -10+b
16 = b
ANSWER: The equation of the line parallel to the given line and passing throught the given point is
y = 5x+16
Question 1210246: can you help me and show me the coordianites on a graph for 2x-3y=12
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The equation is a linear equation, so you only need to plot two points to draw the line.
The other tutor shows one way to find two points by solving the given equation for y, then choosing two convenient values of x to find the corresponding y values, giving the two needed points.
While that method is valid, it is more work than necessary. There is no need to solve the equation for y; it is less work to simply choose "nice" values for the equation in its given form.
Specifically, it is easy to choose x=0 and find the corresponding value of y, and to choose y=0 and find the corresponding value of x. Note that that gives you the x- and y-intercepts of the graph, which might be of particular importance in a particular problem.
x=0:
2(0)-3y=12
-3y=12
y=12/(-3)=-4
One point on the graph is (0,-4)
y=0:
2x-3(0)=12
2x=12
x=6
Another point on the graph is (6,0)
Plot those two points and draw the line containing them.
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
can you help me and show me the coordinates on a graph for 2x-3y=12
~~~~~~~~~~~~~~~~~~~~~
First what you need to know is that it is easy.
It is the easiest thing to learn and to do after learning the multiplication table.
OK, let' start.
From the given equation, 2x - 3y = 12, isolate the term with 'y' on the right side 2x - 12 = 3y.
(you move the term 3y from the left side to the right side, changing the sign;
what you get, 2x - 12 = 3y, is the same as 3y = 2x - 12).
Then you divide all the terms by 3, and you get y = 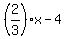 .
In this formula, take x= 0, for simplicity. You will get y = .
In this formula, take x= 0, for simplicity. You will get y = 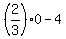 = 0 - 4 = -4.
Next, take x = 3. You will get y = = 0 - 4 = -4.
Next, take x = 3. You will get y =  = 2 - 4 = -2.
You make the table
x | y
------+-------
0 | -4
3 | -2
So, you have two points. One point is (x,y) = (0,-4). The other point is (x,y) = (3,-2).
You can depict/show these point in the graph paper.
Having two points on a paper, you can draw a straight line through these points, using straightedge and a pencil.
This line is the plot you want to get. = 2 - 4 = -2.
You make the table
x | y
------+-------
0 | -4
3 | -2
So, you have two points. One point is (x,y) = (0,-4). The other point is (x,y) = (3,-2).
You can depict/show these point in the graph paper.
Having two points on a paper, you can draw a straight line through these points, using straightedge and a pencil.
This line is the plot you want to get.
Solved.
-------------------------
On how to depict a point, given by its coordinates, on graph paper, see this Youtube video
https://www.youtube.com/watch?v=XlqZBW4F3YA
Question 1210214: (10, y) and (3,4): m=-2/7
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Informally, instead of using formal mathematics -- hoping it will help you understand the formal math....
The slope, "rise over run", is -2/7. That means that whenever x changes by 7 ("the run is 7"), y changes by -2 ("the rise is -2").
From (3,4) to (10,y), x changes by 10-3 = 7 (the run is 7), so the y should change by -2 (the rise is -2). A rise of -2 starting from y=4 puts you at y=2 (4 plus -2 equals 2).
ANSWER: 2
Answer by ikleyn(52786)   (Show Source): (Show Source):
Question 1209916: Hello
I know how to solve this equation but when I insert 7/8 for x. I'm not getting 9.
Can you provide the steps when x is 7/8?
Thanks in advance.
2(4x+1)=9
8x+2=9
8x=7
x=7/8
Found 2 solutions by Edwin McCravy, mccravyedwin:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
Answer by mccravyedwin(407)   (Show Source): (Show Source):
Question 1171415: Write the standard form for this equation.
slope=3/2, y-intercept
Answer by ikleyn(52786)   (Show Source): (Show Source):
Question 1172310: In a design of a highway, a survey for the hill side shows that it is in the following
Formulae :
a) Y= 2X-3 ; Y given the value of X BETWEEN -3.5 TO + 5.5 . State the typical standard straight line formula; Draw Straight Line GRAPH for the two formula and Find the steps in the ratio the Y value of the Gradient.
b) 2Y= 8X-1 ; given the value of X BETWEEN -3.2 TO + 6.3 . State the typical standard straight line formula; Draw Straight Line GRAPH for the formula and Find the steps in the ratio the Y value of the Gradient.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely! Let's break down each part of the problem.
**a) Y = 2X - 3**
1. **Standard Straight Line Formula:**
* The typical standard straight-line formula is y = mx + b, where:
* m is the slope (gradient) of the line.
* b is the y-intercept (the value of y when x = 0).
* In this case, y = 2x - 3, so:
* m = 2
* b = -3
2. **Straight Line Graph:**
* To draw the graph, you can:
* Choose a few values of x within the given range (-3.5 to 5.5).
* Calculate the corresponding y values.
* Plot the points (x, y) on a coordinate plane.
* Draw a straight line through the points.
* Here's how to calculate a couple of points.
* if x = 0, y = 2(0) - 3 = -3. (0, -3)
* if x = 1, y = 2(1) - 3 = -1. (1, -1)
3. **Steps in the Ratio of the Y Value of the Gradient:**
* The gradient (slope) is 2. This means that for every 1 unit increase in x, y increases by 2 units.
* The ratio of the change in y to the change in x is 2/1.
**b) 2Y = 8X - 1**
1. **Standard Straight Line Formula:**
* First, we need to rearrange the equation to the standard form (y = mx + b):
* 2y = 8x - 1
* y = 4x - 1/2
* Now, we can identify:
* m = 4
* b = -1/2
2. **Straight Line Graph:**
* Similar to part a, choose x values within the range (-3.2 to 6.3), calculate y values, and plot the points.
* Here are a few points.
* if x = 0, y = 4(0) - 1/2 = -1/2 (0, -0.5)
* if x = 1, y = 4(1) - 1/2 = 3.5 (1, 3.5)
3. **Steps in the Ratio of the Y Value of the Gradient:**
* The gradient (slope) is 4. This means that for every 1 unit increase in x, y increases by 4 units.
* The ratio of the change in y to the change in x is 4/1.
**Gradient Comparison**
* The gradient of the first line (y = 2x - 3) is 2.
* The gradient of the second line (y = 4x - 1/2) is 4.
* The second line has a steeper slope than the first line.
* The second line's gradient is twice that of the first line. (4/2 = 2)
Question 1173267: Shown below is the solution to the linear program for finding Player A's optimal mixed strategy in a two-person, zero-sum game.
OBJECTIVE FUNCTION VALUE = 3.500
VARIABLE
VALUE
REDUCED COSTS
PA1
0.050
0.000
PA2
0.600
0.000
PA3
0.350
0.000
GAINA
3.500
0.000
CONSTRAINT
SLACK/SURPLUS
DUAL PRICES
1
0.000
−0.500
2
0.000
−0.500
3
0.000
0.000
4
0.000
3.500
a.
What is Player A's optimal mixed strategy?
b.
What is Player B's optimal mixed strategy?
c.
What is Player A's expected gain?
d.
What is Player B's expected loss?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down the information from the linear program output to answer each question:
**a. Player A's Optimal Mixed Strategy**
* **PA1 = 0.050:** Player A should play strategy 1 with a probability of 0.05 (or 5%).
* **PA2 = 0.600:** Player A should play strategy 2 with a probability of 0.60 (or 60%).
* **PA3 = 0.350:** Player A should play strategy 3 with a probability of 0.35 (or 35%).
Therefore, Player A's optimal mixed strategy is (0.05, 0.60, 0.35).
**b. Player B's Optimal Mixed Strategy**
To find Player B's optimal mixed strategy, we look at the **DUAL PRICES** of the constraints. These represent the optimal probabilities for Player B's strategies.
* Constraint 1's Dual Price = -0.500
* Constraint 2's Dual Price = -0.500
* Constraint 3's Dual Price = 0.000
However, the Dual Prices must be converted into positive values, and then normalized, as they represent the negative of the player B's strategy.
Also, the dual prices represent the negative of the player B's strategy, and the 4th constraint represents the gain.
Therefore, the dual prices of constraints 1,2, and 3 are the negative of the probabilities of player B's strategies.
To normalize the dual prices, we must take the absolute value of the dual prices. Then add them together.
0.5 + 0.5 + 0 = 1
Then we can divide each dual price by the sum.
* Player B strategy 1: 0.5/1 = 0.5
* Player B strategy 2: 0.5/1 = 0.5
* Player B strategy 3: 0/1 = 0
Therefore, Player B's optimal mixed strategy is (0.5, 0.5, 0).
**c. Player A's Expected Gain**
* **OBJECTIVE FUNCTION VALUE = 3.500**
* **GAINA = 3.500**
Player A's expected gain is 3.5.
**d. Player B's Expected Loss**
In a zero-sum game, Player B's expected loss is equal to Player A's expected gain.
Therefore, Player B's expected loss is also 3.5.
Question 1174253: The unit cost per gizmo is $30,the fixed cost for making gizmos is $1,200. 60 gizmos must be sold in order to break even.
-Find linear cost function
-Find linear revenue function
-Find linear profit function
Show work with all steps
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely! Let's break down this problem step-by-step.
**1. Linear Cost Function (C(x))**
* **Fixed Cost:** $1,200
* **Unit Cost:** $30 per gizmo
* **x:** Number of gizmos produced
The linear cost function is the sum of the fixed cost and the variable cost (unit cost multiplied by the number of gizmos):
* C(x) = Fixed Cost + (Unit Cost * x)
* C(x) = 1200 + 30x
**2. Linear Revenue Function (R(x))**
* **Break-even Point:** 60 gizmos
* At the break-even point, total revenue equals total cost.
First, let's find the total cost at the break-even point:
* C(60) = 1200 + 30(60)
* C(60) = 1200 + 1800
* C(60) = 3000
Since revenue equals cost at the break-even point:
* R(60) = 3000
Now, let's find the selling price per gizmo:
* Selling Price = Total Revenue / Number of Gizmos
* Selling Price = 3000 / 60
* Selling Price = 50
Therefore, the linear revenue function is:
* R(x) = Selling Price * x
* R(x) = 50x
**3. Linear Profit Function (P(x))**
* Profit is the difference between revenue and cost:
* P(x) = R(x) - C(x)
* P(x) = 50x - (1200 + 30x)
* P(x) = 50x - 1200 - 30x
* P(x) = 20x - 1200
**Summary**
* **Linear Cost Function:** C(x) = 1200 + 30x
* **Linear Revenue Function:** R(x) = 50x
* **Linear Profit Function:** P(x) = 20x - 1200
Question 1174381: Cost, Revenue & Profit
For these problems, x will represent the number of items and y will represent the money.
The fixed costs for a certain item are $165 per week. The cost to produce each item is $3 per item.
Using this information, what is the cost equation? Give your answer in slope-intercept form:
The retailer intends to sell each item for $10/item.
Using this information, what is the revenue equation? Give your answer in slope-intercept form:
If in this week 28 items are made, and all items are sold in the week, what are the total costs to the retailer?
Cost = $
What is the revenue from selling 28 items?
Revenue = $
Finally, what is the profit for this retailer?
Profit = $
Box 1 & 2: Enter your answer as an expression. Example: 3x^2+1, x/5, (a+b)/c
Be sure your variables match those in the question.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve the problems:
**1. Cost Equation**
* Fixed costs: $165
* Variable cost per item: $3
* Cost equation: y = 3x + 165
**2. Revenue Equation**
* Selling price per item: $10
* Revenue equation: y = 10x
**3. Total Costs for 28 Items**
* Total costs = 165 + (3 * 28) = 165 + 84 = $249
**4. Revenue from Selling 28 Items**
* Revenue = 10 * 28 = $280
**5. Profit**
* Profit = Revenue - Total Costs = 280 - 249 = $31
**Answers:**
* Cost equation: 3x + 165
* Revenue equation: 10x
* Cost = $249
* Revenue = $280
* Profit = $31
Question 1173214: Shown below is the solution to the linear program for finding Player A's optimal mixed strategy in a two-person, zero-sum game.
OBJECTIVE FUNCTION VALUE = 3.500
VARIABLE
VALUE
REDUCED COSTS
PA1
0.050
0.000
PA2
0.600
0.000
PA3
0.350
0.000
GAINA
3.500
0.000
CONSTRAINT
SLACK/SURPLUS
DUAL PRICES
1
0.000
−0.500
2
0.000
−0.500
3
0.000
0.000
4
0.000
3.500
a.
What is Player A's optimal mixed strategy?
b.
What is Player B's optimal mixed strategy?
c.
What is Player A's expected gain?
d.
What is Player B's expected loss?
Answer by ikleyn(52786)   (Show Source): (Show Source):
Question 1176614: A school board is investigating various ways of composing faculty for a proposed
new elementary school. They can hire both teachers and aides. The amount of
money spent on salaries each year depends on how many teachers and aides are
hired. The board finds that the average teacher’s salary is $30,000 and the average
aide’s salary is $20,000. Suppose the board finds the following requirements
concerning the permissible number of teachers and aides:
The building can accommodate no more than 50 faculty members
A minimum of 20 faculty members is needed to staff the school
The school cannot be run entirely by aids: there must be at least 12 teachers
For a proper teacher-to-aide ratio, the number of teachers must be at least
two-thirds the number of aides.
It is impossible to hire a negative number of teachers or aides
Find the number of teachers and aides that could be hired that would minimize the
cost to the
district.
Objective Function (Cost): C =
____________________________
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's set up and solve this linear programming problem.
**1. Define Variables**
* Let 't' be the number of teachers.
* Let 'a' be the number of aides.
**2. Formulate the Objective Function (Cost)**
The objective is to minimize the cost. The cost function (C) is:
* C = 30000t + 20000a
**3. Formulate the Constraints**
* **Total Faculty Constraint:** t + a ≤ 50
* **Minimum Faculty Constraint:** t + a ≥ 20
* **Minimum Teachers Constraint:** t ≥ 12
* **Teacher-to-Aide Ratio Constraint:** t ≥ (2/3)a
* **Non-negativity Constraints:** t ≥ 0, a ≥ 0
**4. Simplify the Teacher-to-Aide Ratio Constraint**
* 3t ≥ 2a
* a ≤ (3/2)t
**5. Find the Corner Points**
We need to graph the constraints and find the intersection points.
* **Constraint 1 (t + a ≤ 50):** a ≤ 50 - t
* **Constraint 2 (t + a ≥ 20):** a ≥ 20 - t
* **Constraint 3 (t ≥ 12):** Vertical line at t = 12
* **Constraint 4 (a ≤ (3/2)t):** a ≤ 1.5t
Let's find the intersections:
* **Intersection of t = 12 and a = 20 - t:** a = 20 - 12 = 8. Point (12, 8)
* **Intersection of t = 12 and a = 1.5t:** a = 1.5 * 12 = 18. Point (12, 18)
* **Intersection of t = 12 and a = 50 - t:** a = 50 - 12 = 38. Point (12, 38)
* **Intersection of a = 1.5t and a = 50 - t:** 1.5t = 50 - t, 2.5t = 50, t = 20, a = 1.5 * 20 = 30. Point (20, 30)
* **Intersection of a = 20 - t and a = 1.5t:** 20 - t = 1.5t, 20 = 2.5t, t = 8. This violates t>=12. Therefore, this intersection is not in the feasible region.
* **Intersection of a = 20 - t and a = 50 - t:** Not possible, as they are parallel.
The corner points of the feasible region are:
* (12, 8)
* (12, 18)
* (12, 38)
* (20, 30)
**6. Evaluate the Objective Function at Each Corner Point**
* **(12, 8):** C = 30000(12) + 20000(8) = 360000 + 160000 = 520000
* **(12, 18):** C = 30000(12) + 20000(18) = 360000 + 360000 = 720000
* **(12, 38):** C = 30000(12) + 20000(38) = 360000 + 760000 = 1120000
* **(20, 30):** C = 30000(20) + 20000(30) = 600000 + 600000 = 1200000
**7. Determine the Minimum Cost**
The minimum cost is $520,000, which occurs at the point (12, 8).
**Answers**
* **Teachers:** 12
* **Aides:** 8
* **Objective Function (Cost):** C = 30000t + 20000a
Question 1176842: Many people believe that there is a negative relationship between the amount of time students play video games each week and their GPA.
x 10 3 0 2 5 4 7
y 1.5 2.4 3.2 3.5 2.7 3 2.1
Write the regression equation below. Round all numbers to four decimal places.
y hat =
Using the data shown above, predict a student's GPA when the student plays video games for 15 hours each week. Round your final answer to two decimal places.
What percentage of variation in GPAs can be explained by the number of hours students' play video games each week? Round your final answer to two decimal places.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve this step-by-step.
**1. Calculate the Regression Equation**
We need to find the equation of the form ŷ = a + bx, where:
* x = hours playing video games
* y = GPA
* b = slope
* a = y-intercept
First, calculate the necessary sums:
* Σx = 10 + 3 + 0 + 2 + 5 + 4 + 7 = 31
* Σy = 1.5 + 2.4 + 3.2 + 3.5 + 2.7 + 3 + 2.1 = 18.4
* Σx² = 100 + 9 + 0 + 4 + 25 + 16 + 49 = 203
* Σy² = 2.25 + 5.76 + 10.24 + 12.25 + 7.29 + 9 + 4.41 = 51.2
* Σxy = 15 + 7.2 + 0 + 7 + 13.5 + 12 + 14.7 = 69.4
* n = 7 (number of data points)
Now, calculate b (slope):
* b = (nΣxy - ΣxΣy) / (nΣx² - (Σx)²)
* b = (7 * 69.4 - 31 * 18.4) / (7 * 203 - 31²)
* b = (485.8 - 570.4) / (1421 - 961)
* b = -84.6 / 460
* b ≈ -0.1839
Next, calculate a (y-intercept):
* a = (Σy - bΣx) / n
* a = (18.4 - (-0.1839) * 31) / 7
* a = (18.4 + 5.6999) / 7
* a = 24.0999 / 7
* a ≈ 3.4428
Therefore, the regression equation is:
* ŷ = 3.4428 - 0.1839x
**2. Predict GPA for 15 Hours of Video Games**
* x = 15
* ŷ = 3.4428 - 0.1839 * 15
* ŷ = 3.4428 - 2.7585
* ŷ ≈ 0.6843
Rounded to two decimal places, the predicted GPA is 0.68.
**3. Calculate the Coefficient of Determination (R²)**
R² represents the percentage of variation in GPAs explained by the number of hours playing video games.
First, calculate the correlation coefficient (r):
* r = (nΣxy - ΣxΣy) / √((nΣx² - (Σx)²)(nΣy² - (Σy)²))
* r = -84.6 / √((460)(7 * 51.2 - 18.4²))
* r = -84.6 / √((460)(358.4 - 338.56))
* r = -84.6 / √((460)(19.84))
* r = -84.6 / √9126.4
* r = -84.6 / 95.5322
* r ≈ -0.8856
Now, calculate R²:
* R² = r²
* R² = (-0.8856)²
* R² ≈ 0.7843
Expressed as a percentage and rounded to two decimal places:
* R² ≈ 78.43%
**Answers**
* **Regression equation:** ŷ = 3.4428 - 0.1839x
* **Predicted GPA (15 hours):** 0.68
* **Percentage of variation explained:** 78.43%
Question 1176942: Many people believe that there is a negative relationship between the amount of time students play video games each week and their GPA.
x 10 3 0 2 5 4 7
y 1.5 2.4 3.2 3.5 2.7 3 2.1
Using the data shown above, predict a student's GPA when the student plays video games for 15 hours each week. Round your final answer to two decimal places.
What percentage of variation in GPAs can be explained by the number of hours students' play video games each week? Round your final answer to two decimal places.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Linear Regression**
We'll use linear regression to model the relationship between video game hours (x) and GPA (y).
* **Calculate the means:**
* Mean of x (x̄): (10 + 3 + 0 + 2 + 5 + 4 + 7) / 7 = 31 / 7 ≈ 4.43
* Mean of y (ȳ): (1.5 + 2.4 + 3.2 + 3.5 + 2.7 + 3 + 2.1) / 7 = 18.4 / 7 ≈ 2.63
* **Calculate the sums:**
* Σ(x - x̄)(y - ȳ):
* (10 - 4.43)(1.5 - 2.63) + (3 - 4.43)(2.4 - 2.63) + (0 - 4.43)(3.2 - 2.63) + (2 - 4.43)(3.5 - 2.63) + (5 - 4.43)(2.7 - 2.63) + (4 - 4.43)(3 - 2.63) + (7 - 4.43)(2.1 - 2.63) ≈ 6.26 + 0.33 + 2.59 + 2.11 + 0.06 - 0.16 - 1.48 ≈ 9.71
* Σ(x - x̄)²:
* (10 - 4.43)² + (3 - 4.43)² + (0 - 4.43)² + (2 - 4.43)² + (5 - 4.43)² + (4 - 4.43)² + (7 - 4.43)² ≈ 30.91 + 2.04 + 19.62 + 5.90 + 0.33 + 0.18 + 6.59 ≈ 65.57
* **Calculate the slope (b):**
* b = Σ(x - x̄)(y - ȳ) / Σ(x - x̄)² ≈ 9.71 / 65.57 ≈ -0.148
* **Calculate the y-intercept (a):**
* a = ȳ - b * x̄ ≈ 2.63 - (-0.148) * 4.43 ≈ 2.63 + 0.655 ≈ 3.29
* **Regression equation:**
* y = a + bx ≈ 3.29 - 0.148x
**2. Predict GPA for 15 Hours**
* Plug x = 15 into the regression equation:
* y ≈ 3.29 - 0.148 * 15 ≈ 3.29 - 2.22 ≈ 1.07
* Therefore, the predicted GPA for a student playing video games for 15 hours is approximately 1.07.
**3. Coefficient of Determination (R²)**
* **Calculate Σ(y - ȳ)²:**
* (1.5 - 2.63)² + (2.4 - 2.63)² + (3.2 - 2.63)² + (3.5 - 2.63)² + (2.7 - 2.63)² + (3 - 2.63)² + (2.1 - 2.63)² ≈ 1.28 + 0.05 + 0.33 + 0.76 + 0.005 + 0.14 + 0.28 ≈ 2.855
* **Calculate R²:**
* R² = 1 - (Σ(y - ŷ)² / Σ(y - ȳ)²)
* We need to find Σ(y-ŷ)²
* ŷ values are found by inputting all the original x values into the regression equation: y = 3.29 - 0.148x.
* ŷ = [1.81, 2.84, 3.29, 3.00, 2.55, 2.69, 2.25]
* Σ(y-ŷ)² = (1.5-1.81)² + (2.4-2.84)² + (3.2-3.29)² + (3.5-3.00)² + (2.7-2.55)² + (3-2.69)² + (2.1-2.25)² = 0.0961 + 0.1936 + 0.0081 + 0.25 + 0.0225 + 0.0961 + 0.0225 = 0.689
* R² = 1 - (0.689 / 2.855) ≈ 1 - 0.241 ≈ 0.759
* **Percentage of variation:**
* R² * 100% ≈ 75.9%
**Answers**
* **Predicted GPA for 15 hours:** 1.07
* **Percentage of variation explained:** 75.90%
Question 1179365: A Company manufactures two different products, A and B. Each unit of product A costs $6 to produce and each unit of product B costs $4. The Company insists that total costs for the two products be $500.
(a) Define the cost equation which states that the total cost of producing x units of product A and y units of product B equals $500
(b) Assuming the Company has agreed to fill an order for 50 units of product A, how many units of product B should be produced if total costs are to be kept at $500?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve this problem step-by-step:
**(a) Define the Cost Equation:**
* Let 'x' represent the number of units of product A produced.
* Let 'y' represent the number of units of product B produced.
* The cost of producing 'x' units of product A is 6x.
* The cost of producing 'y' units of product B is 4y.
* The total cost is the sum of these costs, which must equal $500.
Therefore, the cost equation is:
**6x + 4y = 500**
**(b) Calculate the Number of Units of Product B:**
* We are given that x = 50.
* Substitute x = 50 into the cost equation:
* 6(50) + 4y = 500
* 300 + 4y = 500
* Solve for y:
* 4y = 500 - 300
* 4y = 200
* y = 200 / 4
* y = 50
**Answer:**
(a) The cost equation is 6x + 4y = 500.
(b) The company should produce 50 units of product B.
Question 1179833: You are attending Thanksgiving at your family member's house and agreed to bring two side dishes with you; potatoes and corn. You are on a budget though and can only spend $30 in total. You determined that you need at least 10 pounds of food to have enough for all your relatives. Potatoes cost $0.75 per pound and corn costs $1 per pound. The preparation time to peel each pound of potatoes is 15 minutes and to shuck each pound of corn takes 9 minutes. You absolutely hate preparing food and want to minimize the amount of time you need for it. Use the variable "p" to represent number of pounds of potatoes and "c" to represent number of pounds of corn.
a) State what your objective function is, in words, and then write out an equation that represents it.
b) Write out your constraints for the cost and quantity as inequalities. There should be 4 constraints in total.
Can you please explain me this homework question step-by step?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Write inequality for total food
p + c >= 10 pounds (1) (total food)
Write inequality for money to be in budget
0.75*p + 1*c <= 30 dollars.
The amount of time is
15p + 9c minutes,
and you want to minimize it.
There are also inequalities of non-negativity
p >= 0, c >= 0.
So, I wrote the inequalities you were asked for.
+--------------------------------------------+
| The solution to the problem is OBVIOUS. |
+--------------------------------------------+
If you want minimize your time, prepare 10 pounds of corn
and do not touch potatoes.
Question 1180957: A local dairy association enlists the help of a marketing research firm to predict the demand for milk. The research firm finds that the local demand for milk can be predicted the equation q=-4000p+10000, where p represents the price quarter and q represents the number of quarters purchased per week.
Graph the equation.
Identify the slope and q intercept.
Interpret the meaning of slope and q intercept in this application.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to analyze the milk demand equation:
**1. Graphing the Equation:**
The equation q = -4000p + 10000 is a linear equation, so its graph will be a straight line. To graph it, we can find two points and connect them. The easiest points to find are the intercepts:
* **q-intercept:** This is where p = 0. Substituting p = 0 into the equation gives q = -4000(0) + 10000 = 10000. So, the q-intercept is (0, 10000).
* **p-intercept:** This is where q = 0. Substituting q = 0 into the equation gives 0 = -4000p + 10000. Solving for p, we get 4000p = 10000, so p = 10000 / 4000 = 2.5. So, the p-intercept is (2.5, 0).
Plot these two points (0, 10000) and (2.5, 0) on a graph where the horizontal axis is 'p' (price) and the vertical axis is 'q' (quantity). Connect the points with a straight line. Since price and quantity are usually non-negative, you only need to show the first quadrant of the graph.
**2. Identifying the Slope and q-intercept:**
* **Slope:** The equation is in the form q = mp + b, where 'm' is the slope and 'b' is the q-intercept. In this case, the slope is -4000.
* **q-intercept:** As we already found, the q-intercept is 10000.
**3. Interpreting the Meaning of Slope and q-intercept:**
* **Slope (-4000):** The slope represents the change in the quantity of milk purchased (q) for every one-unit change in price (p). Specifically, a slope of -4000 means that for every $1 increase in the price per quarter, the quantity of milk purchased decreases by 4000 quarters per week. The negative sign indicates an inverse relationship between price and quantity demanded, which is typical for demand curves.
* **q-intercept (10000):** The q-intercept represents the quantity of milk purchased per week when the price is $0. In other words, if milk were free, the local dairy association could expect to sell 10,000 quarters per week. While this might seem unrealistic, it's a theoretical point on the demand curve. It helps define the curve and it's a useful point to understand the overall demand for milk.
Question 1181198: A piece of machine is purchased for $1,000,000. Accountants of the firm decided to use straight line
method with the machine being depreciated in 12 years and have an estimated salvage value of
$123,000. Letting V is equal to the book value of the machine and t is the age of machine,
a) Determine the function V = f(t)
b) Determine the book value of machine after 8 years & 11.5 years by using the function
determined in part a
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to determine the function for the book value and calculate the book value after 8 and 11.5 years:
**a) Determine the function V = f(t):**
1. **Calculate the annual depreciation:**
* Depreciable amount = Purchase price - Salvage value
* Depreciable amount = $1,000,000 - $123,000 = $877,000
* Annual depreciation = Depreciable amount / Useful life
* Annual depreciation = $877,000 / 12 years = $73,083.33 per year (approximately)
2. **Write the function:**
Since we're using straight-line depreciation, the book value decreases linearly over time. The function will be in the form:
V(t) = Initial book value - (Annual depreciation * t)
V(t) = $1,000,000 - $73,083.33t
**b) Determine the book value after 8 years and 11.5 years:**
Using the function V(t) = $1,000,000 - $73,083.33t:
* **After 8 years:**
V(8) = $1,000,000 - ($73,083.33 * 8)
V(8) = $1,000,000 - $584,666.64
V(8) = $415,333.36
* **After 11.5 years:**
V(11.5) = $1,000,000 - ($73,083.33 * 11.5)
V(11.5) = $1,000,000 - $840,458.295
V(11.5) = $159,541.705
**Answers:**
* a) The function V = f(t) is: V(t) = $1,000,000 - $73,083.33t
* b) The book value after 8 years is approximately $415,333.36.
* b) The book value after 11.5 years is approximately $159,541.71.
Question 1186028: Find the equation of the ellipse whose center is at (2, 7), having a focus at (2, 10), and having an endpoint of its minor axis at (4, 7).
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to find the equation of the ellipse:
**1. Identify the center:**
The center of the ellipse is given as (h, k) = (2, 7).
**2. Determine the orientation:**
Since the focus (2, 10) and the center (2, 7) have the same x-coordinate, the major axis is vertical.
**3. Find the distance from the center to a focus (c):**
c = |10 - 7| = 3
**4. Find the length of the semi-minor axis (b):**
The endpoint of the minor axis is (4, 7). The distance from the center (2, 7) to this endpoint is the length of the semi-minor axis (b).
b = |4 - 2| = 2
**5. Find the length of the semi-major axis (a):**
We know that a² = b² + c². Therefore:
a² = 2² + 3²
a² = 4 + 9
a² = 13
a = √13
**6. Write the equation of the ellipse:**
The standard form equation of an ellipse with a vertical major axis is:
((x - h)² / b²) + ((y - k)² / a²) = 1
Substituting the values we found:
((x - 2)² / 2²) + ((y - 7)² / (√13)²) = 1
Simplifying:
((x - 2)² / 4) + ((y - 7)² / 13) = 1
Therefore, the equation of the ellipse is $\boxed{\frac{(x-2)^2}{4} + \frac{(y-7)^2}{13} = 1}$.
Question 1186203: A food factory is making a beverage for a customer from mixing two different existing products A and B. The compositions of A and B and prices ($/L) are given as follows,
Amount (L) in /100 L of A and B
Lime Orange Mango Cost ($/L)
A 3 6 4 3
B 7 4 8 11
The customer requires that there must be at least 5 Litres (L) Orange and at least 5Litres of Mango concentrate per 100 Litres of the beverage respectively, but no morethan 6 Litres of Lime concentrate per 100 Litres of beverage. The customer needs atleast 100 Litres of the beverage per week.
(a) Explain why a linear programming model would be suitable for this case study
(b) Formulate a Linear Programming (LP) model for the factory that minimises the total cost of producing the beverage while satisfying all constraints.
(c) Use the graphical method to nd the optimal solution. Show the feasible region andthe optimal solution on the graph. Annotate all lines on your graph. What is the mini-mal cost for the product?
Note: you can use graphical solvers available online but make sure that your graph isclear, all variables involved are clearly represented and annotated, and each line is clearlymarked and related to the corresponding equation.
(d) Is there a range for the cost ($) of A that can be changed without a ecting the opti-mum solution obtained above
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to approach this linear programming problem:
**(a) Suitability of Linear Programming:**
A linear programming model is suitable for this case study because:
1. **Linearity:** The relationships between the amounts of products A and B and the amounts of lime, orange, and mango concentrates are linear. The cost function is also linear.
2. **Optimization:** The problem seeks to minimize the cost, which is a typical objective of linear programming.
3. **Constraints:** There are specific constraints on the amounts of each concentrate and the total volume of the beverage, which can be expressed as linear inequalities.
4. **Divisibility:** The amounts of products A and B can be considered divisible (fractions of liters are possible).
5. **Non-negativity:** The amounts of products A and B cannot be negative.
**(b) Linear Programming Model:**
**Decision Variables:**
* x = Liters of product A per 100L of beverage
* y = Liters of product B per 100L of beverage
**Objective Function (Minimize Cost):**
Cost (C) = 3x + 11y
**Constraints:**
* Orange: 6x + 4y ≥ 5
* Mango: 4x + 8y ≥ 5
* Lime: 3x + 7y ≤ 6
* Total Volume (per 100L): x + y = 100
* Non-negativity: x ≥ 0, y ≥ 0
Since the total volume is *exactly* 100L, the x and y values will directly represent the liters of each product per 100L of beverage.
**(c) Graphical Solution:**
1. **Graph the constraints:** Plot each constraint on a graph with x and y axes. Treat each inequality as an equality to draw the lines, and then shade the appropriate region.
* 6x + 4y = 5 => y = (5 - 6x) / 4
* 4x + 8y = 5 => y = (5 - 4x) / 8
* 3x + 7y = 6 => y = (6 - 3x) / 7
* x + y = 100
2. **Identify the feasible region:** The feasible region is the area where all constraints are satisfied. It will be a polygon bounded by the constraint lines.
3. **Find the vertices:** The vertices are the intersection points of the constraint lines that bound the feasible region. Solve the systems of equations for each intersecting pair of lines. The relevant vertices will be where the orange, mango, and lime constraints intersect with each other and the x+y=100 line.
4. **Evaluate the objective function at each vertex:** Substitute the x and y values of each vertex into the cost function C = 3x + 11y.
5. **Optimal Solution:** The vertex that yields the lowest cost is the optimal solution.
*Intersection points and cost calculations:*
*6x+4y=5 and 4x+8y=5:* solving gives x=0.25, y=0.875, Cost = 3(0.25) + 11(0.875) = $10.4375
*6x+4y=5 and 3x+7y=6:* solving gives x=0.45, y=0.55, Cost = 3(0.45) + 11(0.55) = $7.4
*4x+8y=5 and 3x+7y=6:* solving gives x=1.1, y=0.075, Cost = 3(1.1) + 11(0.075) = $4.025
The minimum cost is $4.025.
**(d) Range for Cost of A:**
To determine the range for the cost of A without affecting the optimal solution, we need to consider the slopes of the objective function and the binding constraints (the constraints that determine the optimal solution).
1. **Binding Constraints:** The binding constraints are the ones that intersect at the optimal solution. In this case, it will be the intersection of 4x+8y=5 and 3x+7y=6.
2. **Slope of the Objective Function:** The slope of the objective function C = 3x + 11y is -3/11.
3. **Slopes of the Binding Constraints:** The slopes of the binding constraints are -4/8 = -1/2 and -3/7.
4. **Range:** The cost coefficient of A can vary as long as the slope of the objective function stays between the slopes of the binding constraints. So, the range of the cost of A (let's call it 'a') will be:
-1/2 <= -a/11 <= -3/7
Multiplying by -11 and flipping the inequalities:
11/2 >= a >= 33/7
5.5 >= a >= 4.71
So, the cost of A can range from $4.71 to $5.5 without changing the optimal solution.
Question 1186852: LINEAR PROGRAMMING
The campus store sells dessert, Sobolo drink and Brukina drink. The Sobolo cost GH₵1.90 and the Brukina cost GH₵2.25. They sell the Sobolo drink for GH₵5.00 and the Burukina for GH₵6.00. They can obtain no more than 100 Sobolo and 75 Burukina per week. To meet the demands, they have to sell a total of at least 120 of the two drinks together. They cannot package more than 150 per week.
(i) Formulate this problem in terms of determining the profit- maximizing combination of the two drinks.
(ii) Solve the problem graphically.
(iii) How many of each should they sell to maximize profit?
(iv) Which constraints are binding?
(v) Determine the slack materials
(vi) Interpret your answers obtained in (v) above.
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
LINEAR PROGRAMMING
The campus store sells dessert, Sobolo drink and Brukina drink.
The Sobolo cost GH₵1.90 and the Brukina cost GH₵2.25.
They sell the Sobolo drink for GH₵5.00 and the Brukina for GH₵6.00.
They can obtain no more than 100 Sobolo and 75 Brukina per week.
To meet the demands, they have to sell a total of at least 120 of the two drinks together.
They cannot package more than 150 per week.
(i) Formulate this problem in terms of determining the profit- maximizing combination of the two drinks.
(ii) Solve the problem graphically.
(iii) How many of each should they sell to maximize profit?
(iv) Which constraints are binding?
(v) Determine the slack materials
(vi) Interpret your answers obtained in (v) above.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This problem is very simple and admits very simple MENTAL solution.
This mental solution is much more educative than formal Linear Programming solution.
Therefore, I place here this mental solution, which require common sense and nothing more.
One Sobolo drink creates the profit of 5.00-1.90 = 3.10.
One Brukina drink creates the profit of 6.00-2.25 = 3.75.
So, let's apply the most aggressive strategy: will sell Brukina drinks as many as possible
in accordance with constraints, and then will sell Sobolo drinks as many as possible
in accordance with the remaining constraints.
According to constraints, we can solve 75 Brukina and we can not solve more Brukina due to the constrain 75.
OK, so we sell 75 Brukina.
Then the other constrain (150 for both) says that we can sell only 75 = 150 - 75 Sobolo.
It meets another constraint for Sobolo and for both, so we are OK to do it.
Thus the optimal solution is 75 Brukina and 75 Sobolo, that give the total profit of
75*(3.10 + 3.75) = 513.75.
All other constraints are satisfied.
ANSWER. The optimal solution is 75 Brukina and 75 Sobolo, that give the total profit of GH₵513.75.
Solved.
To further mock the authors, I will notice that in one part of the problem's condition they use the name Brukina,
while in other part of problem's condition they use the name Burukina, so I conclude
that they do not know the right name, and moreover, using a consistent name is not their priority.
To be consistent, I used the name Brukina consistently in the course of my solution.
Question 1189776: Find the interest on the following amounts using 6%-6 day method:
1. P6,500 at 6% for 54 days
2. P1,500 at 6% for 120 days
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! The 6%-60 day method is a shortcut for calculating simple interest when the interest rate is 6% per year. Here's how it works:
**The 6%-60 day Rule**
* **60 days:** At 6% interest, money earns 1% interest in 60 days.
* **6 days:** To find the interest for 6 days, simply move the decimal point in the principal amount three places to the left.
**Calculations**
**1. P6,500 at 6% for 54 days**
* **Interest for 6 days:** Move the decimal point three places to the left in P6,500, which gives you P6.50.
* **Number of 6-day periods in 54 days:** 54 days / 6 days = 9
* **Total interest:** P6.50 * 9 = **P58.50**
**2. P1,500 at 6% for 120 days**
* **Interest for 6 days:** Move the decimal point three places to the left in P1,500, which gives you P1.50.
* **Number of 6-day periods in 120 days:** 120 days / 6 days = 20
* **Total interest:** P1.50 * 20 = **P30.00**
**Important Notes:**
* The 6%-60 day method is an approximation. It assumes a 360-day year, which is slightly different from the actual number of days in a year.
* For precise interest calculations, especially for longer periods or different interest rates, it's best to use the standard simple interest formula:
Interest = Principal x Rate x Time
Question 1192362: Find the equation of the line in standard form.
1.) a = -8 and b = 2
2.) a= 4 and b = 8
3.) m = 5 and b = -8
4.) m = 3 and (5, -2)
5.) (-1, 9) and (-4, 3)
Find the equation of the line in general form.
1.) m = 1/3 and (-4, -8)
2.) m = 2 and b = 5
3.) a= 12 and b = -9
4.) a= 3 and b = 6
5.) (5, 7) and (3, 2)
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Find the equation of the line in standard form.**
* **1.) a = -8 and b = 2**
* Slope-intercept form: y = mx + b
* y = -8x + 2
* Standard form: 8x + y = 2
* **2.) a = 4 and b = 8**
* Slope-intercept form: y = mx + b
* y = 4x + 8
* Standard form: 4x - y = -8
* **3.) m = 5 and b = -8**
* Slope-intercept form: y = mx + b
* y = 5x - 8
* Standard form: 5x - y = 8
* **4.) m = 3 and (5, -2)**
* Find b: -2 = 3(5) + b
* b = -2 - 15
* b = -17
* Slope-intercept form: y = 3x - 17
* Standard form: 3x - y = 17
* **5.) (-1, 9) and (-4, 3)**
* Find slope (m): (y2 - y1) / (x2 - x1) = (3 - 9) / (-4 - (-1)) = -6 / -3 = 2
* Find b: 9 = 2(-1) + b
* b = 11
* Slope-intercept form: y = 2x + 11
* Standard form: 2x - y = -11
**2. Find the equation of the line in general form.**
* **1.) m = 1/3 and (-4, -8)**
* Find b: -8 = (1/3)(-4) + b
* b = -8 + 4/3
* b = -20/3
* Slope-intercept form: y = (1/3)x - 20/3
* Standard form: x - 3y = 20
* **2.) m = 2 and b = 5**
* Slope-intercept form: y = 2x + 5
* Standard form: 2x - y = -5
* **3.) a = 12 and b = -9**
* Slope-intercept form: y = mx + b
* y = 12x - 9
* Standard form: 12x - y = 9
* **4.) a = 3 and b = 6**
* Slope-intercept form: y = mx + b
* y = 3x + 6
* Standard form: 3x - y = -6
* **5.) (5, 7) and (3, 2)**
* Find slope (m): (y2 - y1) / (x2 - x1) = (2 - 7) / (3 - 5) = -5 / -2 = 5/2
* Find b: 7 = (5/2)(5) + b
* b = 7 - 25/2
* b = -11/2
* Slope-intercept form: y = (5/2)x - 11/2
* Standard form: 5x - 2y = 11
Question 1209474: For the straight line defined by points (4,55) and (6,83) determine the slope (m) and the y-intercept (b). Do not round up.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As you go two units to the right from the point (4,55), you go 83-55 = 28 units up along the straight line.
It means that the slope is 28/2 = 14. the ANSWER for the slope
To find y-intercept, you should go 4 units to the left from the point (4,55).
Hence, you should move 14*4 = 56 units down along the straight line.
Thus, y-intercept is at y= 55-56 = -1. the ANSWER for the y-intercept
Solved.
This solution is to make you smile.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The two given points are (4,55) and (6,83). We need to find the slope m and the y-intercept b.
(1) Finding the slope
Informally....
Going from (4,55) to (6,83) we move 2 units (6-4) to the right (positive direction) and 28 units (83-55) up (positive direction). So the slope is 28/2 = 14.
Formally....
slope = rise/run = change in y divided by change in x

ANSWER #1: the slope is m=14
(2) Finding the y-intercept
Informally....
The y-intercept is the y value when x is 0. From the first point (4,55) we need to move 4 units to the left to get to where x is 0. In moving 2 units to the right from (4,55) to (6,83) we moved up 28 units; moving 4 units to the left is twice as far as moving 2 units to the right, and in the opposite direction. So we need to move 2*28=56 units down (in the y direction) from (4,55) to reach the y-axis. 56 units down from y=55 puts us at y=-1. So the y-intercept is -1.
Formally....
The equation is y=mx+b, and we have determined that the slope m is 14. Using that equation with the x and y coordinates of the first point and the slope of 14....




ANSWER #2: the y-intercept is -1
Question 1209384: True or false: the points (4,2) (8,10) and (11,16) are collinear
Found 3 solutions by greenestamps, math_tutor2020, mananth:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The three points are collinear if the slope of the line containing (4,2) and (8,10) is the same as the slope of the line containing (8,10) and (11,16).
Of course you can use the formal formula for finding the slope of the line containing two points. But in my opinion it is more educational to use the informal "rise over run" definition of slope.
Between (4,2) and (8,10) the run is 8-4=4 and the rise is 10-2=8; the slope is rise/run = 8/4 = 2.
Between (8,10) and (11,16) the run is 16-10=6 and the rise is 11-8=3; the slope is rise/run = 6/3 = 2.
The slopes are the same, so the three points are collinear.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Label the points as A,B,C in any order you prefer.
A = (4,2)
B = (8,10)
C = (11,16)
Let's find the slope of line AB.
m = (y2 - y1)/(x2 - x1)
m = (10 - 2)/(8 - 4)
m = 8/4
m = 2
Do the same for line BC
m = (y2 - y1)/(x2 - x1)
m = (16 - 10)/(11 - 8)
m = 6/3
m = 2
Lines AB and BC have the same slope, so the three points are collinear.
Collinear points are on the same straight line.
You can use graphing tools like Desmos and GeoGebra to verify.
The equation of the line that goes through all three points is y = 2x-6
Answer: True
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the pointbes be A (4,2),B (8,10) and C (11,16)
If slope of AB = slope of BC then the points are co linear
If the points are (x1,y1) &(x2,y2) and (x3,y3)
(y3-y2)/(x3-x2) = (y2-y1)/(x2-x1)
(16-10)/(11-8) = 2
(10-2)/(8-4) =2
The points are co linear
Question 1198171: Consider a chef who must plan a banquet. Possible menu items and the cost data presented below:
Item Cost ($) Per Serving
Appetizers
A 0.25
B 0.30
C 0.35
Salads
X 0.25
Y 0.45
Vegetables
P 0.20
Q 0.15
R 0.40
Main Meals
1 1.25
2 2.50
3 3.00
The banquet is to consist of:
A. at least one appetizer;
B. exactly one salad;
C. at least one but no more than two vegetables; and
D. exactly one main meal.
The chef has been advised to select items from the menu which will minimize
total cost of the banquet. All decision variables take the form of the binary
numbers only.
Instructions:
i. Write mathematical form of the inequalities of all the constraints. (5)
ii. Write mathematical form objective function (5)
iii. Tabulate your problem into the solver (5)
iv. Using Excel Solver, solve the problem and interpret your solution (5)
Answer by onyulee(41)  (Show Source): (Show Source):
You can put this solution on YOUR website! Certainly, let's formulate the banquet planning problem and solve it using Excel Solver.
**i. Mathematical Inequalities (Constraints)**
* **Appetizer Constraint:**
* A + B + C ≥ 1
* **Salad Constraint:**
* X + Y = 1
* **Vegetable Constraints:**
* P + Q + R ≥ 1
* P + Q + R ≤ 2
* **Main Meal Constraint:**
* 1 + 2 + 3 = 1
* **Binary Variables:**
* A, B, C, X, Y, P, Q, R, 1, 2, 3 ∈ {0, 1}
**ii. Objective Function (Minimize Cost)**
* Cost = 0.25A + 0.30B + 0.35C + 0.25X + 0.45Y + 0.20P + 0.15Q + 0.40R + 1.25*1 + 2.50*2 + 3.00*3
**iii. Tabulation in Excel Solver**
1. **Set up the Excel Sheet:**
* Create a table with the following columns:
* Item
* Cost
* Decision Variable (Binary)
* List all items (A, B, C, X, Y, P, Q, R, 1, 2, 3) and their corresponding costs.
* In the "Decision Variable" column, enter a cell for each item (e.g., B2 for item A, B3 for item B, etc.).
2. **Define Decision Variables:**
* In the "Decision Variable" cells, enter 0 or 1.
3. **Calculate Total Cost:**
* In a separate cell, use the SUMPRODUCT function to calculate the total cost based on the decision variables and costs:
* `=SUMPRODUCT(B2:B11,C2:C11)`
4. **Set up Constraints:**
* In separate cells, create formulas to represent each constraint:
* Appetizer: `=SUM(B2:B4)`
* Salad: `=SUM(B5:B6)`
* Vegetables: `=SUM(B7:B9)`
* Main Meal: `=SUM(B10:B12)`
5. **Open Solver:**
* Go to "Data" -> "Solver".
6. **Set Objective:**
* Set the "Set Objective" cell to the cell containing the total cost formula.
7. **Select "Min"** to minimize the cost.
8. **By Changing Variable Cells:**
* Select the range of cells containing the decision variables (e.g., B2:B12).
9. **Add Constraints:**
* Click "Add" to add each constraint:
* Appetizer: `=SUM(B2:B4)>=1`
* Salad: `=SUM(B5:B6)=1`
* Vegetables: `=SUM(B7:B9)>=1`
* Vegetables: `=SUM(B7:B9)<=2`
* Main Meal: `=SUM(B10:B12)=1`
* Binary Constraints:
* For each decision variable cell, add a constraint: `B2=0` or `B2=1`
10. **Select Solving Method:**
* Choose "Simplex LP" or "GRG Nonlinear" as the solving method.
11. **Solve:**
* Click "Solve".
**iv. Interpret Solution**
* Solver will find the optimal combination of menu items that minimizes the total cost while satisfying all the constraints.
* The "Decision Variable" cells will indicate which items to include in the banquet (1 = include, 0 = exclude).
* The "Total Cost" cell will display the minimum cost of the banquet.
**Note:**
* The specific steps and interface may vary slightly depending on your Excel version.
* This solution provides a framework. You'll need to adapt it to your specific Excel setup.
By following these steps, you can effectively use Excel Solver to determine the most cost-effective menu for the banquet.
Question 1209272: Write an equation of the line in slope-intercept form.
A line graphed on a coordinate plane. The x-axis ranges from negative 3 to 5, in increments of 1. The y-axis ranges from negative 1 to 7, in increments of 1. The line passes through the points at ordered pair 0 comma 5 and ordered pair 3 comma 4.
An equation is:
Found 3 solutions by greenestamps, MathTherapy, josgarithmetic:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
One of the given points, (0,5), is the y-intercept, so the equation in slope-intercept form is of the form y=mx+5.
Use the coordinates of the other given point to determine the slope m to complete the equation.
You can plug numbers into the equation for calculating the slope. But I think it gives the student a better understanding if you simply use the "rise over run" definition of slope.
From (0,5) to (3,4), you move (3-0) = 3 units in the x direction ("run") and (4-5) = -1 in the y direction ("rise"), so the slope "rise over run" is -1/3.
And then the equation in slope-intercept form of the line through the two given points is
ANSWER: y = (-1/3)x+5
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Write an equation of the line in slope-intercept form.
A line graphed on a coordinate plane. The x-axis ranges from negative 3 to 5, in increments of 1. The y-axis ranges from negative 1 to 7, in increments of 1. The line passes through the points at ordered pair 0 comma 5 and ordered pair 3 comma 4.
An equation is:
He's WRONG. The slope is NOT - 1, as 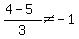 .
Ordered pair: (0, 5) and (3, 4), so m, or slope = .
Ordered pair: (0, 5) and (3, 4), so m, or slope = 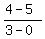 = = 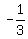 .
Since the y-intercept was given as point (0, 5), we get the CORRECT equation as: .
Since the y-intercept was given as point (0, 5), we get the CORRECT equation as:  .
In order for the graph to show the line, the y-axis can range from - 1 to 7, but the x-axis NEEDS to range
from - 3 to 15, i/o from - 3 to 5, in order for the equation: .
In order for the graph to show the line, the y-axis can range from - 1 to 7, but the x-axis NEEDS to range
from - 3 to 15, i/o from - 3 to 5, in order for the equation:  to be clearly viewed. to be clearly viewed.

Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1198769: what are the 2 points and slope for this question ?
Connor uses a gift card to buy milkshakes for himself and his friends Thursday after he and a friend order the balance on Konners gift card was $22.45 Saturday after he and four friends ordered he had a balance of $6.70 on his card determine the cost of each milkshake.
I need help finding
1 . 2 points
2. rate of change or slope
3. Dependent variable
4 independent variable.
Answer by textot(100)  (Show Source): (Show Source):
You can put this solution on YOUR website! To analyze the situation mathematically, we can represent it as a linear relationship where the balance on the gift card decreases as the number of milkshakes purchased increases.
---
### Step 1: Define Variables
- **Independent Variable**: The number of milkshakes ordered (denoted as \( x \)).
- **Dependent Variable**: The remaining balance on the gift card (denoted as \( y \)).
---
### Step 2: Identify Two Points
We are given:
1. After Connor and one friend (2 milkshakes) ordered, the balance was $22.45. This gives the point \((2, 22.45)\).
2. After Connor and four friends (5 milkshakes) ordered, the balance was $6.70. This gives the point \((5, 6.70)\).
---
### Step 3: Find the Rate of Change (Slope)
The slope represents the rate at which the balance decreases per milkshake:
\[
m = \frac{y_2 - y_1}{x_2 - x_1}
\]
Substitute the points \((2, 22.45)\) and \((5, 6.70)\):
\[
m = \frac{6.70 - 22.45}{5 - 2} = \frac{-15.75}{3} = -5.25
\]
The slope is \( -5.25 \), meaning each milkshake costs **$5.25**.
---
### Step 4: Equation of the Line
Using the point-slope form:
\[
y - y_1 = m(x - x_1)
\]
Substitute \( m = -5.25 \) and \((x_1, y_1) = (2, 22.45)\):
\[
y - 22.45 = -5.25(x - 2)
\]
Simplify:
\[
y = -5.25x + 10.50 + 22.45
\]
\[
y = -5.25x + 32.95
\]
---
### Step 5: Answers
1. **Two points**: \((2, 22.45)\) and \((5, 6.70)\).
2. **Rate of change or slope**: \( -5.25 \), meaning the cost of each milkshake is **$5.25**.
3. **Dependent variable**: The remaining balance on the gift card (\( y \)).
4. **Independent variable**: The number of milkshakes ordered (\( x \)).
Let me know if you'd like further clarification!
Question 1199722: Describe the transformation for this problem. There may be more than one(max you can have with only changes to a and d are three).
Given f(x) = x, describe the transformation for g(x) = -2 • f(x) - 1.
Answer by textot(100)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Vertical Stretch/Compression:**
* **-2 * f(x):** This part of the transformation vertically stretches the graph of f(x) by a factor of 2. The negative sign reflects the graph across the x-axis.
**2. Vertical Shift:**
* **-2 * f(x) - 1:** This part of the transformation shifts the graph of -2 * f(x) vertically downward by 1 unit.
**In summary:**
The graph of g(x) = -2 * f(x) - 1 is obtained from the graph of f(x) by:
1. **Vertically stretching** the graph by a factor of 2.
2. **Reflecting** the graph across the x-axis.
3. **Shifting** the graph 1 unit downward.
Question 1199724: Given f(x) = 3x + 1, and g(x) = -2 • f(x) - 1. Describe the transformations(list them) and write the new simplified equation for g(x).
Answer by textot(100)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Transformations:**
* **Vertical Stretch:** The coefficient -2 stretches the graph of f(x) vertically by a factor of 2.
* **Reflection in the x-axis:** The negative sign in front of -2f(x) reflects the graph of f(x) across the x-axis.
* **Vertical Shift:** The "-1" at the end of the equation shifts the graph of -2f(x) downward by 1 unit.
**2. Simplified Equation for g(x)**
* g(x) = -2 * f(x) - 1
* g(x) = -2 * (3x + 1) - 1
* g(x) = -6x - 2 - 1
* g(x) = -6x - 3
**Therefore:**
* The transformations applied to f(x) to obtain g(x) are: vertical stretch by a factor of 2, reflection in the x-axis, and a vertical shift downward by 1 unit.
* The simplified equation for g(x) is g(x) = -6x - 3.
Question 1209297: Crew a can assemble 2 cars in 5 days, and crew b can assemble 3 cars in 7 days. If both work together assemble 100cars, with crew b working 10 days longer than crew a , how many days must crew be work?
Answer by ikleyn(52786)   (Show Source): (Show Source):
Question 1209244: What is the equation of the line that has a slope of
2 and goes through the point (4,1)?
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Question 1209208:
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1209194: Please help me with this question: https://imgur.com/a/CRaEH2C
It's about displacement/time graphs, velocity/time graphs and acceleration/time graphs
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Please help me with this question: https://imgur.com/a/CRaEH2C
It's about displacement/time graphs, velocity/time graphs and acceleration/time graphs
~~~~~~~~~~~~~~~~~~~~~~~
I will assume that horizontal axis is for the time t, vertical axis is for position y.
(a) Velocity is zero where the derivative 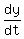 is zero.
They are the points, where the tangent line to the plot is horizontal.
These points are B, D, E, G, I, J.
(b) The acceleration is zero where the second derivative is zero.
They are the points, where the tangent line to the plot is horizontal.
These points are B, D, E, G, I, J.
(b) The acceleration is zero where the second derivative 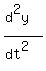 is zero.
These points are the inflection points.
In the plot, they are C, E, H, and some point between I and J, which
is not marked in the plot.
(c) These intervals are BC, DF, GH, IJ.
These intervals are those where the position y of the object becomes closer
to zero as the time increases.
(d) The acceleration is negative where the plot is convex upwards (arcs CDE, HIJ).
The velocity is negative where the derivative is zero.
These points are the inflection points.
In the plot, they are C, E, H, and some point between I and J, which
is not marked in the plot.
(c) These intervals are BC, DF, GH, IJ.
These intervals are those where the position y of the object becomes closer
to zero as the time increases.
(d) The acceleration is negative where the plot is convex upwards (arcs CDE, HIJ).
The velocity is negative where the derivative 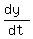 is negative
(Arcs AB, DEFG, IJ).
Both the acceleration is negative and the velocity is negative in intersections
of these sets/arcs DE and IJ.
(e) Regarding first 2.5 seconds,
the body starts (t=0) from the detector position and moves in the "negative"
direction from the detector until getting point B on the graph.
At the start, the starting velocity is negative.
On the curve AB, acceleration is positive, so the magnitude
of the velocity diminishes and the negative velocity steadily
becomes 0 at point B.
After getting point B, the body moves to the detector (curve BC) with positive acceleration,
passes the detector, and further moves from the detector in "positive" direction.
Curve CD describes decelerated movement. The velocity on CD remains positive,
but the magnitude of the velocity steadily diminishes.
At point D, the velocity becomes zero, and the body starts moving to the detector.
At this point, I will stop my story to leave the room for you to think and to describe
the further events on your own. is negative
(Arcs AB, DEFG, IJ).
Both the acceleration is negative and the velocity is negative in intersections
of these sets/arcs DE and IJ.
(e) Regarding first 2.5 seconds,
the body starts (t=0) from the detector position and moves in the "negative"
direction from the detector until getting point B on the graph.
At the start, the starting velocity is negative.
On the curve AB, acceleration is positive, so the magnitude
of the velocity diminishes and the negative velocity steadily
becomes 0 at point B.
After getting point B, the body moves to the detector (curve BC) with positive acceleration,
passes the detector, and further moves from the detector in "positive" direction.
Curve CD describes decelerated movement. The velocity on CD remains positive,
but the magnitude of the velocity steadily diminishes.
At point D, the velocity becomes zero, and the body starts moving to the detector.
At this point, I will stop my story to leave the room for you to think and to describe
the further events on your own.
Analyzing and describing motions using plots is a perfect way to develop
your understanding of processes and terminology in Physics / kinematics.
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790, 11791..11835, 11836..11880, 11881..11925, 11926..11970, 11971..12015, 12016..12060, 12061..12105, 12106..12150, 12151..12195, 12196..12240, 12241..12285, 12286..12330, 12331..12375, 12376..12420, 12421..12465, 12466..12510, 12511..12555, 12556..12600, 12601..12645, 12646..12690, 12691..12735, 12736..12780, 12781..12825, 12826..12870, 12871..12915, 12916..12960, 12961..13005, 13006..13050, 13051..13095, 13096..13140, 13141..13185, 13186..13230, 13231..13275, 13276..13320, 13321..13365, 13366..13410, 13411..13455, 13456..13500, 13501..13545, 13546..13590, 13591..13635, 13636..13680, 13681..13725, 13726..13770, 13771..13815, 13816..13860, 13861..13905, 13906..13950, 13951..13995, 13996..14040, 14041..14085, 14086..14130, 14131..14175, 14176..14220, 14221..14265, 14266..14310, 14311..14355, 14356..14400, 14401..14445, 14446..14490, 14491..14535, 14536..14580, 14581..14625, 14626..14670, 14671..14715, 14716..14760, 14761..14805, 14806..14850, 14851..14895, 14896..14940, 14941..14985, 14986..15030, 15031..15075, 15076..15120, 15121..15165, 15166..15210, 15211..15255, 15256..15300, 15301..15345, 15346..15390, 15391..15435, 15436..15480, 15481..15525, 15526..15570, 15571..15615, 15616..15660, 15661..15705, 15706..15750, 15751..15795, 15796..15840, 15841..15885, 15886..15930, 15931..15975, 15976..16020, 16021..16065, 16066..16110, 16111..16155, 16156..16200, 16201..16245, 16246..16290, 16291..16335, 16336..16380, 16381..16425, 16426..16470, 16471..16515, 16516..16560, 16561..16605, 16606..16650, 16651..16695, 16696..16740, 16741..16785, 16786..16830, 16831..16875, 16876..16920, 16921..16965, 16966..17010, 17011..17055, 17056..17100, 17101..17145, 17146..17190, 17191..17235, 17236..17280, 17281..17325, 17326..17370, 17371..17415, 17416..17460, 17461..17505, 17506..17550, 17551..17595, 17596..17640, 17641..17685, 17686..17730, 17731..17775, 17776..17820, 17821..17865, 17866..17910, 17911..17955, 17956..18000, 18001..18045, 18046..18090, 18091..18135, 18136..18180, 18181..18225, 18226..18270, 18271..18315, 18316..18360, 18361..18405, 18406..18450, 18451..18495, 18496..18540, 18541..18585, 18586..18630, 18631..18675, 18676..18720, 18721..18765, 18766..18810, 18811..18855, 18856..18900, 18901..18945, 18946..18990, 18991..19035, 19036..19080, 19081..19125, 19126..19170, 19171..19215, 19216..19260, 19261..19305, 19306..19350, 19351..19395, 19396..19440, 19441..19485, 19486..19530, 19531..19575, 19576..19620, 19621..19665, 19666..19710, 19711..19755, 19756..19800, 19801..19845, 19846..19890, 19891..19935, 19936..19980, 19981..20025, 20026..20070, 20071..20115, 20116..20160, 20161..20205, 20206..20250, 20251..20295, 20296..20340, 20341..20385, 20386..20430, 20431..20475, 20476..20520, 20521..20565, 20566..20610, 20611..20655, 20656..20700, 20701..20745, 20746..20790, 20791..20835, 20836..20880, 20881..20925, 20926..20970, 20971..21015, 21016..21060, 21061..21105, 21106..21150, 21151..21195, 21196..21240, 21241..21285, 21286..21330, 21331..21375, 21376..21420, 21421..21465, 21466..21510, 21511..21555, 21556..21600, 21601..21645, 21646..21690, 21691..21735, 21736..21780, 21781..21825, 21826..21870, 21871..21915, 21916..21960, 21961..22005, 22006..22050, 22051..22095, 22096..22140, 22141..22185, 22186..22230, 22231..22275, 22276..22320, 22321..22365, 22366..22410, 22411..22455, 22456..22500, 22501..22545, 22546..22590, 22591..22635, 22636..22680, 22681..22725, 22726..22770, 22771..22815, 22816..22860, 22861..22905, 22906..22950, 22951..22995, 22996..23040, 23041..23085, 23086..23130, 23131..23175, 23176..23220, 23221..23265, 23266..23310, 23311..23355, 23356..23400, 23401..23445, 23446..23490, 23491..23535, 23536..23580, 23581..23625, 23626..23670, 23671..23715, 23716..23760, 23761..23805, 23806..23850, 23851..23895, 23896..23940, 23941..23985, 23986..24030, 24031..24075, 24076..24120, 24121..24165, 24166..24210, 24211..24255, 24256..24300, 24301..24345, 24346..24390, 24391..24435, 24436..24480, 24481..24525, 24526..24570, 24571..24615, 24616..24660, 24661..24705, 24706..24750, 24751..24795, 24796..24840, 24841..24885, 24886..24930, 24931..24975, 24976..25020, 25021..25065, 25066..25110, 25111..25155, 25156..25200, 25201..25245, 25246..25290, 25291..25335, 25336..25380, 25381..25425, 25426..25470, 25471..25515, 25516..25560, 25561..25605, 25606..25650, 25651..25695, 25696..25740, 25741..25785, 25786..25830, 25831..25875, 25876..25920, 25921..25965, 25966..26010, 26011..26055, 26056..26100, 26101..26145, 26146..26190, 26191..26235, 26236..26280, 26281..26325, 26326..26370, 26371..26415, 26416..26460, 26461..26505, 26506..26550, 26551..26595, 26596..26640, 26641..26685, 26686..26730, 26731..26775, 26776..26820, 26821..26865, 26866..26910, 26911..26955, 26956..27000, 27001..27045, 27046..27090, 27091..27135, 27136..27180, 27181..27225, 27226..27270, 27271..27315, 27316..27360, 27361..27405, 27406..27450, 27451..27495, 27496..27540, 27541..27585, 27586..27630, 27631..27675, 27676..27720, 27721..27765, 27766..27810, 27811..27855, 27856..27900, 27901..27945, 27946..27990, 27991..28035, 28036..28080, 28081..28125, 28126..28170, 28171..28215, 28216..28260, 28261..28305, 28306..28350, 28351..28395, 28396..28440, 28441..28485, 28486..28530, 28531..28575, 28576..28620, 28621..28665, 28666..28710, 28711..28755, 28756..28800, 28801..28845, 28846..28890, 28891..28935, 28936..28980, 28981..29025, 29026..29070, 29071..29115, 29116..29160, 29161..29205, 29206..29250, 29251..29295, 29296..29340, 29341..29385, 29386..29430, 29431..29475, 29476..29520, 29521..29565, 29566..29610, 29611..29655, 29656..29700, 29701..29745, 29746..29790, 29791..29835, 29836..29880, 29881..29925, 29926..29970, 29971..30015, 30016..30060, 30061..30105, 30106..30150, 30151..30195, 30196..30240, 30241..30285, 30286..30330, 30331..30375, 30376..30420, 30421..30465, 30466..30510, 30511..30555, 30556..30600, 30601..30645, 30646..30690, 30691..30735, 30736..30780, 30781..30825, 30826..30870, 30871..30915, 30916..30960, 30961..31005, 31006..31050, 31051..31095, 31096..31140, 31141..31185, 31186..31230, 31231..31275, 31276..31320, 31321..31365, 31366..31410, 31411..31455, 31456..31500, 31501..31545, 31546..31590, 31591..31635, 31636..31680, 31681..31725, 31726..31770, 31771..31815, 31816..31860, 31861..31905, 31906..31950, 31951..31995, 31996..32040, 32041..32085, 32086..32130, 32131..32175, 32176..32220, 32221..32265, 32266..32310, 32311..32355, 32356..32400, 32401..32445, 32446..32490, 32491..32535, 32536..32580, 32581..32625, 32626..32670, 32671..32715, 32716..32760, 32761..32805, 32806..32850, 32851..32895, 32896..32940, 32941..32985, 32986..33030, 33031..33075, 33076..33120, 33121..33165, 33166..33210, 33211..33255, 33256..33300, 33301..33345, 33346..33390, 33391..33435, 33436..33480, 33481..33525, 33526..33570, 33571..33615, 33616..33660, 33661..33705, 33706..33750, 33751..33795, 33796..33840, 33841..33885, 33886..33930, 33931..33975, 33976..34020, 34021..34065, 34066..34110, 34111..34155, 34156..34200, 34201..34245, 34246..34290, 34291..34335, 34336..34380, 34381..34425, 34426..34470, 34471..34515, 34516..34560, 34561..34605, 34606..34650, 34651..34695, 34696..34740, 34741..34785, 34786..34830, 34831..34875, 34876..34920, 34921..34965, 34966..35010, 35011..35055, 35056..35100, 35101..35145, 35146..35190, 35191..35235, 35236..35280, 35281..35325, 35326..35370, 35371..35415, 35416..35460, 35461..35505, 35506..35550, 35551..35595, 35596..35640, 35641..35685, 35686..35730, 35731..35775, 35776..35820, 35821..35865, 35866..35910, 35911..35955, 35956..36000, 36001..36045
|
| |





