|
Question 957359: two perpendicular lines intersect at J(-3,-3). one line is given by the equation y=7/4x - 9/4 .
Determine the equation of the other line in point-slope form and in slope-intercept form.
Please Kindly help me, I'm stuck !
Found 2 solutions by Theo, lwsshak3:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! slope of perpendicular line is equal to negative reciprocal of slope of the line that it is perpendicular to.
7/4 becomes -4/7
slope intercept form of the equation is y = mx + b
replace m with -4/7 and you get:
y = -4/7 * x + b
point that the line goes through is (-3,-3)
point slope form of the equation is y - y1 = m * (x - x1)
replace m with -4/7 and replace y1 with -3 and replace x with -3 and you get:
y + 3 = -4/7 * (x + 3).
convert this equation to slope intercept form and you get:
y = -4/7 * x - 33/7
the equations of your original line and the line perpendicular to it are:
y = 7/4 * x - 9/4
y = -4/7 * x + 9/7
when you graph these equations, you will see that they do ***** NOT ***** intersect at the point (-3,-3).
the reason is because the equation of your original line is not correct.
you show it as y = 7/4 * x - 9/4.
it should have been y = 7/4 * x + 9/4.
a slight error that makes all the difference in the world.
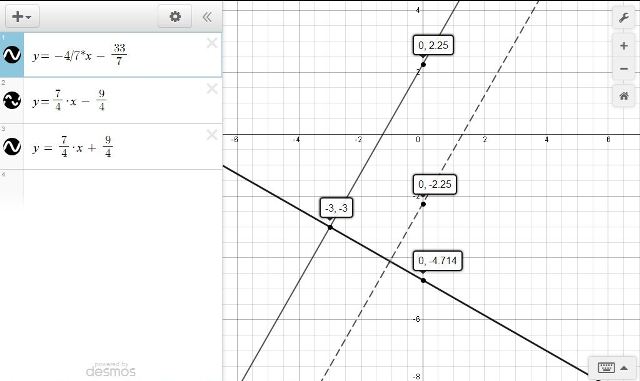
you can see this on the graph.
the dashed line is your original equation of y = 7/4 * x - 9/4
the solid black lines are the correct equations.
y = 7/4 * x + 9/4 is what should have been the original equation and y = -4/7 * x + -33/7 is the equation of the line perpendicular to it.
how do you tell which line is which on the graph?
you look for the y-intercept point and the general direction of the line.
the line of y = 7/4 * x + 9/4 slopes up from left to right and crosses the y-axis at y = 9/4 which is equivalent to y = 2.25.
the line of y = -4/7 * x - 33/7 slopes down from left to right and crosses the y-axis at y = -33/7 which is equivalent to y = -4.714.
your original equation of y = 7/4 * x - 9/4 slopes upward from left to right and is crossing the y-axis at y = -9/4 which is equivalent to y = -2.25.
here's the graph:
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! two perpendicular lines intersect at J(-3,-3). one line is given by the equation y=7/4x - 9/4 .
Determine the equation of the other line in point-slope form and in slope-intercept form.
***
y=7/4x - 9/4
slope=7/4
slope of perpendicular line=-4/7(negative reciprocal)
equation: y=-4x/7+b
solve for b using given coordinates of the point of intersection(-3,-3)
-3=-4*-3/7+b
b=-3-12/7=-21/7-12/7=-33/7
equation: y=-4x/7-33/7
..
note: Given equation (y=7/4x - 9/4) does not go thru point (-3,-3).
So, problem is not set up correctly.
Equation should be (y=7/4x+9/4) which goes thru (-3,-3)
Please let me know whether or not i am correct
|
|
|
| |