|
Question 932586: Hello,
I think I'm mixing something up in the question below.
Write the general form of the equation of the circle with radius r and center (h,k).
r= 2 sqrt( 3 ) (h, k) = (4, -4)
This is what I came up with
(x-4)^2 + (y + 4)^2 = 6
which gives
x^2-8x+16 + y^2+8y+16
then
x^2+y^2-8x+8y+32=6
then I get confused after I subtract 32 from both sides
x^2+y^2-8x+8y=-26
Found 2 solutions by ewatrrr, stanbon:
Answer by ewatrrr(24785)   (Show Source):
You can put this solution on YOUR website! Standard Form of an Equation of a Circle is 
........
(x-4)^2 + (y + 4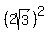)^2 =  = 12
(x-4)^2 + (y + 4)^2 = 12 is the Standard Form of the Circle
Answer by stanbon(75887)  (Show Source):
You can put this solution on YOUR website! I think I'm mixing something up in the question below.
Write the general form of the equation of the circle with radius r and center (h,k).
r= 2 sqrt( 3 ) (h, k) = (4, -4)
This is what I came up with
(x-4)^2 + (y + 4)^2 = (2sqrt(3))^2
(x-4)^2 + (y+4)^2 = 12
Comment::
I think either of the 2 equations above is the answer
the problem is looking for.
Cheers,
Stan H.
------------------------
The rest of this does not give the "general form".
--------------------------
which gives
x^2-8x+16 + y^2+8y+16 = 12
then
x^2+y^2-8x+8y+32=12
then I get confused after I subtract 32 from both sides
x^2+y^2-8x+8y = -20
----
Cheers,
Stan H.
|
|
|
| |
