Question 922472: I can't find an equation for the following ordered pairs (1,1), (2,5), (3,14), (4,30) etc. I know that I am adding the square of each x-value number to the previous y-value but I'm confused about the equation.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
As you observed, the nth term is the sum of the first n squares.
1 = 1²
5 = 1²+2²
14 = 1²+2²+3²
30 = 1²+2²+3²+4²
So the nth term is 1²+2²+3²+...+n²
That should be related to the sum 1+2+3+...+n
1+2+3+...+n is the sum of an arithmetic series with a1=1 and d=1
Using the formula for the sum of the an arithmetic series to n terms:
1+2+3+...+n = 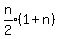 or or  Let's divide each term of our sequence by the sum of the
first n natural numbers, and see if we get a recognizable
pattern:
1/(1) = 1
5/(1+2) = 5/3
14/(1+2+3) = 14/6 = 7/3
30/(1+2+3+4) = 30/10 = 3
Now if we write 1 as 3/3 and 3 and 9/3 we do have a
recognizable pattern
3/3, 5/3, 7/3, 9/3, ...
The numerators go 3,5,7,9,... each of which is 1 more than 2,4,6,8,...
which has nth term 2n
So 3,5,7,9, has nth term 2n+1
So 3/3, 5/3, 7/3, 9/3 has nth term (2n+1)/3
Since we got that sequence by DIVIDING our sequence by the sums of the
first n natural numbers, the nth term of our sequence is gotten by
MULTIPLYING those two nth terms. So the nth ordered pair is given
by the equation:
Let's divide each term of our sequence by the sum of the
first n natural numbers, and see if we get a recognizable
pattern:
1/(1) = 1
5/(1+2) = 5/3
14/(1+2+3) = 14/6 = 7/3
30/(1+2+3+4) = 30/10 = 3
Now if we write 1 as 3/3 and 3 and 9/3 we do have a
recognizable pattern
3/3, 5/3, 7/3, 9/3, ...
The numerators go 3,5,7,9,... each of which is 1 more than 2,4,6,8,...
which has nth term 2n
So 3,5,7,9, has nth term 2n+1
So 3/3, 5/3, 7/3, 9/3 has nth term (2n+1)/3
Since we got that sequence by DIVIDING our sequence by the sums of the
first n natural numbers, the nth term of our sequence is gotten by
MULTIPLYING those two nth terms. So the nth ordered pair is given
by the equation:
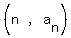  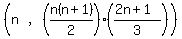 or
or
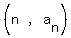  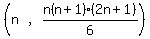 Edwin
Edwin
|
|
|