SOLUTION: I need help solving each system. Thank you. 2x-y-z=1 x+2y+z=0 3x-y-2x=-1

Algebra ->  Linear-equations -> SOLUTION: I need help solving each system. Thank you. 2x-y-z=1 x+2y+z=0 3x-y-2x=-1      Log On


   

Question 886137: I need help solving each system. Thank you.
2x-y-z=1
x+2y+z=0
3x-y-2x=-1
Found 2 solutions by josgarithmetic, richwmiller:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
Put into matrix form and use elementary row operations to convert into an upper triangular arrangement.

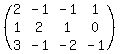
%28matrix%283%2C4%2C2%2C-1%2C-1%2C1%2C1%2C2%2C1%2C0%2C3%2C-1%2C-2%2C-1%29%29

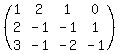
%28matrix%283%2C4%2C1%2C2%2C1%2C0%2C2%2C-1%2C-1%2C1%2C3%2C-1%2C-2%2C-1%29%29

%28matrix%283%2C4%2C1%2C2%2C1%2C0%2C0%2C-5%2C-3%2C1%2C0%2C-7%2C-5%2C-1%29%29, R2-2*R1, R3-3*R1

%28%28matrix%283%2C4%2C1%2C2%2C1%2C0%2C0%2C5%2C3%2C1%2C0%2C7%2C5%2C1%29%29%29, multiply row 2 and 3 by -1

%28%28matrix%283%2C4%2C1%2C2%2C1%2C0%2C0%2C35%2C21%2C7%2C0%2C35%2C25%2C5%29%29%29, 7*R2, 5*R3


%28matrix%283%2C4%2C1%2C2%2C1%2C0%2C0%2C5%2C3%2C1%2C0%2C0%2C2%2C1%29%29, (1/7)R2, (1/2)R3

This can continue using subtraction to eliminate elements above the diagonal. This is already in a form that says, z=-1%2F2, and you can use this to back substitute and solve for the next variables one at a time.

%28matrix%283%2C4%2C1%2C2%2C1%2C0%2C0%2C5%2C3%2C1%2C0%2C0%2C1%2C-1%2F2%29%29, R3 divid by 2

%28matrix%283%2C4%2C1%2C2%2C0%2C1%2F2%2C0%2C5%2C0%2C5%2F2%2C0%2C0%2C1%2C-1%2F2%29%29, R2-3R3, R1-R3

%28matrix%283%2C4%2C1%2C2%2C0%2C1%2F2%2C0%2C1%2C0%2C1%2F2%2C0%2C0%2C1%2C-1%2F2%29%29, Divide R2 by 5

And next do R1-2*R2, ... and your matrix tells you the solution.

After so much long, detailed work, I believe I see a mistake...
hopefully you can understand the process being shown and can check and reduce the matrix on paper and be sure of the correct answers.

REDONE ON PAPER:
Tracing the work between paper and the (wrongly) posted solution is difficult. Let me just post here my redone RESULT solution matrix; likely some of the arithmetic computation was wrong in computing one of the elements.
This one should be right...
%28matrix%283%2C4%2C1%2C0%2C0%2C2%2F11%2C0%2C1%2C-5%2F11%2C0%2C0%2C1%2C12%2F11%29%29
---
Rendering is failing at the moment.
x=2%2F11
y=-7%2F11
z=12%2F11

Answer by richwmiller(17219) About Me  (Show Source):
You can put this solution on YOUR website!
2,-1,-1,1
1,2,1,0
3,-1,-2,-1
divide row 1 by 2/1
1,-1/2,-1/2,1/2
1,2,1,0
3,-1,-2,-1
add down (-1/1) *row 1 to row 2
1,-1/2,-1/2,1/2
0,5/2,3/2,-1/2
3,-1,-2,-1
add down (-3/1) *row 1 to row 3
1,-1/2,-1/2,1/2
0,5/2,3/2,-1/2
0,1/2,-1/2,-5/2
divide row 2 by 5/2
1,-1/2,-1/2,1/2
0,1,6/10,-2/10
0,1/2,-1/2,-5/2
add down (-1/2) *row 2 to row 3
1,-1/2,-1/2,1/2
0,1,3/5,-1/5
0,0,-16/20,-48/20
divide row 3 by -4/5
1,-1/2,-1/2,1/2
0,1,3/5,-1/5
0,0,1,3
We now have the value for the last variable.
We will work our way up and get the other solutions.
add up (-3/5) *row 3 to row 2
1,-1/2,-1/2,1/2
0,1,0,-2
0,0,1,3
add up (1/2) *row 3 to row 1
1,-2/4,0,2
0,1,0,-2
0,0,1,3
add up (1/2) *row 2 to row 1
1,0,0,1
0,1,0,-2
0,0,1,3
final
1,0,0,1
0,1,0,-2
0,0,1,3