|
Question 840064: A chemist measured the pressure of a gas in atmospheres at different temperatures in °C:
Temp (°C) -136 -25 0 25 100 273
Pressure(atm) 0.50 0.91 1.00 1.09 1.37 2.00
Can you predict the temperature at which the pressure would equal zero? Please explain how you got to your conclusion.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The data shows that pressure is a linear function of temperature.
PLOTTING THE DATA POINTS to get a graph, you realize that pressure is a linear function of temperature. Your teacher may expect you to plot the data, and "eyeball" a line that goes through all the points.
 From the graph you realize that the points are almost perfectly aligned, so it is a linear function. From the graph you realize that the points are almost perfectly aligned, so it is a linear function.
From the line you may be able to estimate that the point with  (pressure equal zero atmosphere) corresponds to (pressure equal zero atmosphere) corresponds to  ( ( 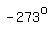  ). ).
You do not need to read that from the graph. Knowing that
as the temperature increases from   to to 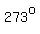  , ,
the pressure increases by 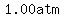 ,from ,from 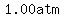 to to 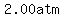 , ,
you would figure out that
as the temperature decreases from   to to 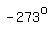  , ,
the pressure will decrease by 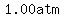 ,from ,from 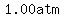 to to 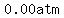 . .
It could also be that your teacher expects you to calculate the slope, using two points, and write the linear function, to find the x intercept.
Using the points for   to to 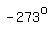  , ,
 . .
We know the y-intercept is  , since the , since the  (pressure) for (pressure) for   is is 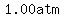 , so the linear function is , so the linear function is
 or or  . .
Hopefully you are not expected to go into statistic calculations.
QUICK ANSWER, WITHOUT PLOTTING, AND WITHOUT A CALCULATOR:
You see that as the temperature increases by 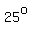  degrees degrees
(from 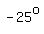  to to   or from or from   to to  ), ),
the pressure increases by 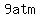 , ,
and for a temperature increases 4 times as large
(   increase, from increase, from   to to   ), ),
the pressure increases by about 4 times as much, 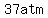 . .
The rate of increase (the slope of the line) seems to be about 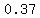 atmosphere per degree. atmosphere per degree.
You also see that the increase in pressure for a temperature increase of 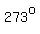  is is 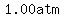 , ,
and for half as large a change in temperature (from 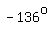  to to   ), ),
the pressure increases by half as much, 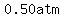 . .
You could calculate the slope from   to to 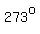  to verify that it is also about to verify that it is also about 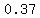 , but that takes time. , but that takes time.
nowing that
as the temperature increases from   to to 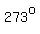  , ,
the pressure increases by 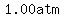 ,from ,from 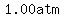 to to 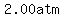 , ,
you would figure out that
as the temperature decreases from   to to 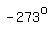  , ,
the pressure will decrease by 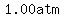 ,from ,from 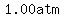 to to 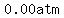 , ,
without ever using a calculator or pencil and paper.
NOTE:
As a non-famous chemist of the 20th-21st centuries, I would not extrapolate that far out of the data range to draw a conclusion.
Besides, they taught me that in the 9th grade, in physics and chemistry classes.
A physicist in the 1700's would draw a conclusion from such limited data as he could obtain at the time. If he was a famous and respected scientist, people would eventually believe him, and his conclusion would become a law of physics named after him that would be included in physics and chemistry textbooks.
|
|
|
| |