5y-25x-5 = 0
You have to get it in the form
y = x + or y = x - ,
where there are numbers in those boxes.
It's called the "(slope)(y-intercept)" form and is usually written
y = mx + b where m is a number which is the slope (how steep the line
is and the y-intercept is the point (0,b).
To get
5y-25x-5 = 0 in that form. First we isolate the y-term which is 5y
We add +25x and +5 to both sides:
5y-25x-5 = 0
+25x+5 +25x+5
-----------------
5y = 25x+5
That give us
5y = 25x+5
Now we want to get just y on both sides, so we divide all the numbers
on both sides by 5
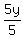



 Then we simplify by canceling:
1 5 1
Then we simplify by canceling:
1 5 1
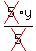

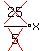

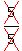 1 1 1
And you get
y = 5x + 1
Next you compare that to
y = mx + b
So m is 5 and b is 1 and so the slope, m, is 5 and the
y-intercept is the point (0,1). And the graph is a line
that rises 5 units for every unit is runs to the right.
And it crosses the y-axis at the point (0,1)
1 1 1
And you get
y = 5x + 1
Next you compare that to
y = mx + b
So m is 5 and b is 1 and so the slope, m, is 5 and the
y-intercept is the point (0,1). And the graph is a line
that rises 5 units for every unit is runs to the right.
And it crosses the y-axis at the point (0,1)
 The black line is the graph of the line. You will notice that
it crosses the y-axis at the y-intercept (0,1). You will also
notice that the green lines show that the black line rises 5
units for every 1 unit that it "runs" to the right. (The
green lines are not part of the graph, I put them in to show
that the vertical green line is the "rise" and the horizontal
line is the "run". The slope always equals the rise over the run,
which is the coefficient of x on the right side of the equation.
Edwin
The black line is the graph of the line. You will notice that
it crosses the y-axis at the y-intercept (0,1). You will also
notice that the green lines show that the black line rises 5
units for every 1 unit that it "runs" to the right. (The
green lines are not part of the graph, I put them in to show
that the vertical green line is the "rise" and the horizontal
line is the "run". The slope always equals the rise over the run,
which is the coefficient of x on the right side of the equation.
Edwin