|
Question 82171: Hello out there,I need some help with some slope problems that is giving me a hard time,the first one is,Write the point-slope form of the line that passes through (3,-3)and (5,1).The second one is,Write an equation in slope-intercept form of the line having the given slope and passing through the given point:m=o,(0,-3).The next one is,Write the equation in slope-intercept form of the passing through each pair of points:(6,-2)and (3,-4).The last one is,Write the equation in slope-intercept form of the line passing through each pair of points:(-8,2)and (0,6),thanks for whoever can help.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! note: if you need more help with finding an equation through 2 points check out this solver
"Write the point-slope form of the line that passes through (3,-3)and (5,1)"
| Solved by pluggable solver: Finding the Equation of a Line |
First lets find the slope through the points ( , , ) and ( ) and ( , , ) )
 Start with the slope formula (note: ( Start with the slope formula (note: ( , , ) is the first point ( ) is the first point ( , , ) and ( ) and ( , , ) is the second point ( ) is the second point ( , , )) ))
 Plug in Plug in  , , , , , , (these are the coordinates of given points) (these are the coordinates of given points)
 Subtract the terms in the numerator Subtract the terms in the numerator 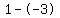 to get to get  . Subtract the terms in the denominator . Subtract the terms in the denominator 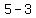 to get to get 
 Reduce Reduce
So the slope is

------------------------------------------------
Now let's use the point-slope formula to find the equation of the line:
------Point-Slope Formula------
 where where  is the slope, and ( is the slope, and ( , , ) is one of the given points ) is one of the given points
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Rewrite Rewrite 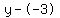 as as 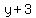
 Distribute Distribute 
 Multiply Multiply  and and  to get to get 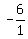 . Now reduce . Now reduce 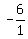 to get to get 
 Subtract Subtract  from both sides to isolate y from both sides to isolate y
 Combine like terms Combine like terms  and and  to get to get 
------------------------------------------------------------------------------------------------------------
Answer:
So the equation of the line which goes through the points ( , , ) and ( ) and ( , , ) is: ) is:
The equation is now in  form (which is slope-intercept form) where the slope is form (which is slope-intercept form) where the slope is  and the y-intercept is and the y-intercept is 
Notice if we graph the equation  and plot the points ( and plot the points ( , , ) and ( ) and ( , , ), we get this: (note: if you need help with graphing, check out this solver) ), we get this: (note: if you need help with graphing, check out this solver)
 Graph of Graph of  through the points ( through the points ( , , ) and ( ) and ( , , ) )
Notice how the two points lie on the line. This graphically verifies our answer.
|
"The second one is,Write an equation in slope-intercept form of the line having the given slope and passing through the given point:m=0,(0,-3)"
| Solved by pluggable solver: FIND a line by slope and one point |
What we know about the line whose equation we are trying to find out:
- it goes through point (0, -3)
- it has a slope of 0
First, let's draw a diagram of the coordinate system with point (0, -3) plotted with a little blue dot:

Write this down: the formula for the equation, given point  and intercept a, is and intercept a, is
 (see a paragraph below explaining why this formula is correct) (see a paragraph below explaining why this formula is correct)
Given that a=0, and  , we have the equation of the line: , we have the equation of the line:

Explanation: Why did we use formula  ? Explanation goes here. We are trying to find equation y=ax+b. The value of slope (a) is already given to us. We need to find b. If a point ( ? Explanation goes here. We are trying to find equation y=ax+b. The value of slope (a) is already given to us. We need to find b. If a point ( , ,  ) lies on the line, it means that it satisfies the equation of the line. So, our equation holds for ( ) lies on the line, it means that it satisfies the equation of the line. So, our equation holds for ( , ,  ): ):  Here, we know a, Here, we know a,  , and , and  , and do not know b. It is easy to find out: , and do not know b. It is easy to find out:  . So, then, the equation of the line is: . So, then, the equation of the line is:  . .
Here's the graph:

|
note: its hard to see, but its a horizontal line going through (0,-3)
"The next one is,Write the equation in slope-intercept form of the passing through each pair of points:(6,-2)and (3,-4)"
| Solved by pluggable solver: Finding the Equation of a Line |
First lets find the slope through the points ( , , ) and ( ) and ( , , ) )
 Start with the slope formula (note: ( Start with the slope formula (note: ( , , ) is the first point ( ) is the first point ( , , ) and ( ) and ( , , ) is the second point ( ) is the second point ( , , )) ))
 Plug in Plug in  , , , , , , (these are the coordinates of given points) (these are the coordinates of given points)
 Subtract the terms in the numerator Subtract the terms in the numerator 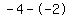 to get to get  . Subtract the terms in the denominator . Subtract the terms in the denominator 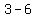 to get to get 
 Reduce Reduce
So the slope is

------------------------------------------------
Now let's use the point-slope formula to find the equation of the line:
------Point-Slope Formula------
 where where  is the slope, and ( is the slope, and ( , , ) is one of the given points ) is one of the given points
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Rewrite Rewrite 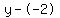 as as 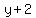
 Distribute Distribute 
 Multiply Multiply  and and  to get to get  . Now reduce . Now reduce  to get to get 
 Subtract Subtract  from both sides to isolate y from both sides to isolate y
 Combine like terms Combine like terms  and and  to get to get 
------------------------------------------------------------------------------------------------------------
Answer:
So the equation of the line which goes through the points ( , , ) and ( ) and ( , , ) is: ) is:
The equation is now in  form (which is slope-intercept form) where the slope is form (which is slope-intercept form) where the slope is  and the y-intercept is and the y-intercept is 
Notice if we graph the equation  and plot the points ( and plot the points ( , , ) and ( ) and ( , , ), we get this: (note: if you need help with graphing, check out this solver) ), we get this: (note: if you need help with graphing, check out this solver)
 Graph of Graph of  through the points ( through the points ( , , ) and ( ) and ( , , ) )
Notice how the two points lie on the line. This graphically verifies our answer.
|
"Write the equation in slope-intercept form of the line passing through each pair of points:(-8,2)and (0,6)"
| Solved by pluggable solver: Finding the Equation of a Line |
First lets find the slope through the points ( , , ) and ( ) and ( , , ) )
 Start with the slope formula (note: ( Start with the slope formula (note: ( , , ) is the first point ( ) is the first point ( , , ) and ( ) and ( , , ) is the second point ( ) is the second point ( , , )) ))
 Plug in Plug in  , , , , , , (these are the coordinates of given points) (these are the coordinates of given points)
 Subtract the terms in the numerator Subtract the terms in the numerator 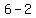 to get to get  . Subtract the terms in the denominator . Subtract the terms in the denominator 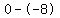 to get to get 
 Reduce Reduce
So the slope is

------------------------------------------------
Now let's use the point-slope formula to find the equation of the line:
------Point-Slope Formula------
 where where  is the slope, and ( is the slope, and ( , , ) is one of the given points ) is one of the given points
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Rewrite Rewrite 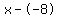 as as 
 Distribute Distribute 
 Multiply Multiply  and and  to get to get 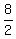 . Now reduce . Now reduce 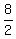 to get to get 
 Add Add  to both sides to isolate y to both sides to isolate y
 Combine like terms Combine like terms  and and  to get to get 
------------------------------------------------------------------------------------------------------------
Answer:
So the equation of the line which goes through the points ( , , ) and ( ) and ( , , ) is: ) is:
The equation is now in  form (which is slope-intercept form) where the slope is form (which is slope-intercept form) where the slope is  and the y-intercept is and the y-intercept is 
Notice if we graph the equation  and plot the points ( and plot the points ( , , ) and ( ) and ( , , ), we get this: (note: if you need help with graphing, check out this solver) ), we get this: (note: if you need help with graphing, check out this solver)
 Graph of Graph of  through the points ( through the points ( , , ) and ( ) and ( , , ) )
Notice how the two points lie on the line. This graphically verifies our answer.
|
|
|
|
| |