|
Question 821639: I don't know what kind of problem this is...please help!
Sketch a quadratic function with zeros at -3 and 1. I don't understand the "zeros at -3 and 1" part.
Found 2 solutions by josmiceli, KMST:
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! This problem does not require much work, because there are many correct answers.
You do not need much information or calculations to do that sketch.
You need information to understand the question.
Knowing the meaning of some words used by math teachers helps.
For example a quadratic function is a polynomial function of degree 2, meaning something like
 or or  . .
The graph of a quadratic function is a curve called a parabola, with a more or less pointy "end" called the vertex of the parabola.
It also helps if you know some tricks old mathematicians used to solve similar problems, but you should understand how they figured it out, or at least why those procedures work.
One of many functions with zeros at -3 and 1 is

It is a quadratic function that
becomes zero when  because the first factor is zero, and because the first factor is zero, and
becomes zero when  because the second factor is zero. because the second factor is zero.
So  and and  are called zeros of the function. are called zeros of the function.
You could write that function in the factored form,

or in the standard polynomial form,

or in the vertex form,
 . .
All quadratic functions can be written in the standard form and in the vertex form.
If the zeros are rational numbers, there is also a nice-looking factored form.
In that case, it can be proven that the  at the vertex is the average of the zeros. at the vertex is the average of the zeros.
So the  at the vertex is at the vertex is  , ,
and then  at the vertex can be found by substituting at the vertex can be found by substituting  for for  in one of the forms of the equation for that function. in one of the forms of the equation for that function.
There are many other quadratic functions with the same zeros,
because multiplying 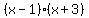 times some non-zero number does not change where the product is zero. times some non-zero number does not change where the product is zero.
For example  is another quadratic function with zeros at -3 and 1. Its graph is is another quadratic function with zeros at -3 and 1. Its graph is 
So is  with the graph with the graph 
Multiplying times a factor may change the value of  at the vertex, but not the zeros or the at the vertex, but not the zeros or the  at the vertex. at the vertex.
So any graph that you sketch looking like that (crossing the x-axis at -3 and 1, and symmetrical to both sides of  may be a good answer. may be a good answer.
EXTRA:
The vertex form is the most useful form of the equation if you want to sketch the graph of a particular function,
because it tells you the vertex position.
The minimum value for  is is  , and happens when , and happens when  <--> <--> <--> <--> <--> <-->
For all other values of  , , 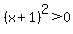 and and  . .
That point, with  and and  is the vertex of the graph. is the vertex of the graph.
|
|
|
| |