SOLUTION: are any of these liner or not and why? 2x+3=1 2x=5 6x^2-3=4

Algebra ->  Linear-equations -> SOLUTION: are any of these liner or not and why? 2x+3=1 2x=5 6x^2-3=4       Log On


   

Question 778005: are any of these liner or not and why?
2x+3=1
2x=5
6x^2-3=4
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Strange question. I expected to se a y somewhere, but there is none.

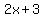2x%2B3 can be called a linear polynomial, or a linear binomial.
In an x-y plane, 2x%2B3=1 <--> 2x=1-3 <--> 2x=-2 <--> x=-1 is the equation of the vertical line shown below.
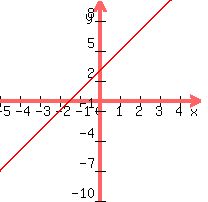
drawing%28200%2C200%2C-3%2C3%2C-3%2C3%2Cgrid%280%29%2Cline%28-1%2C-3%2C-1%2C3%29%29, while y=2x%2B3 graphs as graph%28200%2C200%2C-5%2C5%2C-10%2C10%2C2x%2B3%29
y=2x%2B3 is a linear equation, can be called a linear function.
On the other hand, 2x%2B3=1 or x=-1 does not show a linear relation ship between x and y.
The value of x is fixed.
The value of y is anything, not depending on a variable x.

Something similar can be said of 2x=5 <--> x=5%2F2.

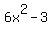6x%5E2-3 can be called a quadratic polynomial, or a quadratic binomial, because it is a polynomial of degree 2.
It cannot be called linear.
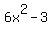6x%5E2-3 has an x%5E2, and the term linear is reserved for polynomials where there is no visible exponent on the one variable.

6x%5E2-3=4 <--> 6x%5E2=4%2B7 <--> 6x%5E2=11 <--> x%5E2=11%2F6 <--> system%28x=sqrt%2811%2F6%29%2Cx=-sqrt%2811%2F6%29%29
In an x-y plane that would graph as two vertical lines.