|
Question 761587: Assume that you sell two sizes of storage sheds: large and small. The large size requires 12 feet of lumber and takes 3 hours to build. The small size requires 8 feet of lumber and takes 1 hour to build. You can use 48 feet of lumber each day and plan to spend at most 9 hours per day to build the sheds.
a. Model the situation above. Your algebraic model should be a system of four inequalities.
b. You sell the large sheds for $70 each and the small ones for $30 each. What numbers of each kind should you make per day in order to maximize your income?
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! EDIT: ADJUSTING FOR A MISUNDERSTANDING...
EDITED AGAIN...
The question you might want to be able to answer in part a for the sheds is, how many of each shed can be built.
Large shed, 12 feet, 3 hours
Small shed, 8 feet, 1 hour
Restrictions: 48 feet per day, no more than 9 days.
Let x = how many small sheds
let y = how many large sheds
The restriction indicates {48 feet/day}/{ 9 hours/days} = 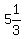 feet per hour. feet per hour.
Account for feet, converted to days needed (EDITED):
(8*x+12*y)/(1/48)= number of days
Account for time:
(1*x+3*y)(1/9)= number of days.
The description still needs, ...? Otherwise, the problem description is not complete. You ALMOST have enough information for two equations for a system, but do not quite have all the information yet. ?
After second edit, we seem to have a general accounting for feet to days, and another accounting for hours to days. We apparantly have two equations in two unknowns; maybe needing to be inequalities. BUT we need two more.
|
|
|
| |