|
Question 734629: a swimming pool is being emptied by a pump that removes water at a constant rate. After 1 hour the pool contains 8,000 gallons and after 4 hours 2,000 gallons.
a. How fast is the pump removing water.
b. Find the slope intercept form of a line that models the amount of water in the pool. Interpret the slope.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! a. The first question can be answered the fifth grader way, without mentioning algebra.
The pump removed  in the time between those two measurements. in the time between those two measurements.
The time elapsed between those two measurements was 
The pump is removing water at a rate of
 
b.  = volume of water in the pool (in gallons) = volume of water in the pool (in gallons)
 = time since the emptying started (in hours) = time since the emptying started (in hours)
(You could use  for volume in the pool and for volume in the pool and  for time if you like that better). for time if you like that better).
You need to write the linear function that models the emptying of the pool, showing  as a function of as a function of  . .
You have two points from that line: point 1 and point 2,
 (1,8000) and (1,8000) and  (4,2000), (4,2000),
meaning that for  , ,  and and
for  , ,  . .
Equation of the line:
There is more than one "form" for the equation of a line, and an infinite number of versions of some of those forms, but the slope-intercept form is very popular and comes in just one unique version.
The slope-intercept form looks like 
with the values  and and  being constants that determine the line. being constants that determine the line.
ONE WAY TO GET TO THE EQUATION OF THE LINE:
If you are very good at solving systems of equations, you could use that skill to find the equation.
You could substitute the coordinates of P[1] into  to get to get
 --> -->  and and
you could substitute the coordinates of P[2] into  to get to get
 --> --> 
and then you could solve  to find to find  and and  . .
ANOTHER WAY:
Using what you just learned about linear functions, you can calculate the slope as the change in y divided by the change in x when we go from point 1 to point 2:

So far this is the same calculation as for part a, but involving algebra and talking about lines and slope.
After finding the slope, you could use one of the points and the concept of slope (or the formula for the point-slope form of the equation to write the equation of the line in point-slope form. Then you could "solve for  to get to the slope intercept form. to get to the slope intercept form.
The definition of slope,  , using a point ( , using a point ( , , ) representing any point in the line, and a known point A( ) representing any point in the line, and a known point A(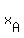 , ,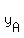 ) and the formula for a point-slope form of the equation are related to each other like this: ) and the formula for a point-slope form of the equation are related to each other like this:
 <---> <---> 
Using  and point (1,8000) we can write and point (1,8000) we can write
 as the point-slope form as the point-slope form
Then,
 --> -->  --> -->  --> --> 
At time  , the moment the pump was turned on to start emptying the pool, the volume of water in the pool was , the moment the pump was turned on to start emptying the pool, the volume of water in the pool was . There were 10,000 gallons of water in the pool. That is the y-intercept, the point where the line intercepts the y-axis. . There were 10,000 gallons of water in the pool. That is the y-intercept, the point where the line intercepts the y-axis.

INTERPRETING THE SLOPE:
The slope is the rate of increase of y as x increases, and it means that for every increase of 1 hour in the time  spent emptying the pool, the volume spent emptying the pool, the volume  of water in the pool increases by of water in the pool increases by 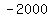 gallons. The negative sign for that "increase" in the volume shows that the volume is really decreasing. gallons. The negative sign for that "increase" in the volume shows that the volume is really decreasing.
|
|
|
| |