|
Question 708695: What are 5 points that satisfy the equation 5y+3x=-13 ?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! In theory, you could give either variable a value and solve for the other variable to get one point.
You would do it again for each additional point.
Or you could solve for one variable as a function of the other,
and get a formula:
 --> -->  --> --> 
For any value of x, that formula makes it easy to calculate the corresponding value for y.
Examples:
 --> -->  --> -->  gives you point (0,-13/5) gives you point (0,-13/5)
 --> -->  --> -->  --> -->  gives you point (0,-16/5) gives you point (0,-16/5)
However, for this equation, with those coefficients in front of x and y,
you will end up with a lot of fractions, and may not like the results,
especially if you need to use those points for a graph.
If you want an integer value for  you need you need 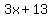 to be a multiple of 5, to be a multiple of 5,
and since  you would want you would want  to be a multiple of 5, to be a multiple of 5,
like  --> --> 
 --> -->  --> -->  --> -->  --> -->  gives you point (4,-5). gives you point (4,-5).
If you do not need to "show your work" you could get additional points easily using a graph,
without further calculations.
If you need or want to keep calculating,
increasing or decreasing  by 5 you will keep getting by 5 you will keep getting  to be a multiple of 5, to be a multiple of 5,
and will keep getting integers for y.
 gives you (9,-8) gives you (9,-8)
 gives you (-1,-2) gives you (-1,-2)
GETTING ADDITIONAL POINTS FROM A GRAPH:
Once you have one point of the line, you can plot it on a graph,
and then you can use the slope of the line to place more points on the graph.
(If you do not need your graph, you may be able to get the same result adding numbers in your head,
or counting on your fingers).
From  , we could solve for y to get , we could solve for y to get  , ,
which made it easy to calculate one point.
We can go further to the  form of the equation form of the equation
 --> --> 
where the coefficient of the x is the slope of the line.
Going from one point in the line to another point in the line,
the slope is the change in y divided by the change in x.
A slope of 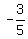 means that means that
an increase of 5 units in x corresponds to
an increase of -3 units (meaning a decrease of 3 units) in y.
We use that fact to go from one point to the next on the graph.

We move 5 units to the right (an increase of 5 for x)
and 3 units down (decrease of 3 for y) to mark the next point.
We can also reverse direction, decreasing x by 5, while increasing y by 3.
So after calculating (4,-5) as a first point, we could go to (9,-8) and (14,-11).
Reversing direction we could go to (-1,-2) and to (-6,1).
Without graphing:
I would just make a table for the x and y values and put the first point I calculate on the table.
In this case, I would put x=4, y=-5 in the middle.
Then I would fill the x values counting by 5's up and down,
and the y values counting by -3 (counting by 3 in the other direction):

|
|
|
| |