|
Question 70283: Please help me with graphing these problems.
I do not understand how to do this.
a y>-2
b y>2x-2
c 4x-6y<12
Thanks
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's one way you can think about these problems.
.
Let's begin by talking our way through:
.
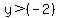
Let's start by presuming that the > sign is an equal sign and the equation actually is
.

.
What does the graph of this equation look like? It is a horizontal line through the point
-2 on the y-axis. Does this make sense? What it says is that no matter what value you
select for x, the value of y will be -2.
.
The reality is that the equal sign was only put in to help us picture what is going on
with the graph. Now we can put the > back into the equation. Now we can tell that the
values of y must be greater than -2. This means that y is allowed to be any value
above the line that is the graph. You can shade that entire region, but only the region
that is ABOVE the line. y can be any value in the shaded region. However, y cannot have
the value -2 because y is only allowed to be GREATER than -2. Therefore, y can NOT be
on the line.
.
The next problem says that:
.
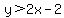
.
Like we did before, let's temporarily replace the > sign with an equal sign. This changes
the equation to:
.

.
This is in the slope-intercept form. Maybe you can picture the graph. It crosses the
y-axis at -2 and it slopes up and to the right at a rate of +2. That means for every 1 unit
you move horizontally to the right you go vertically up 2 units. You know that (0,-2) which
is the y-axis intercept is on the graph. You can easily find another point on the graph
by setting y = 0 in the line equation and then solving the equation for the corresponding
value of x:
.

.
When you solve this you find that x = 2 is the answer. Therefore, you know that (2,0) is a
second point on the graph. With the two points (0,-2) and (2,0) plotted you can draw a line
through them and you will have the graph of 
.
At this point you should replace the = sign with the > sign to get back to the original
problem. This form tells you that y can only have values ABOVE the graph because y
must be greater than the values in the line. Shade the entire region above the line.
The shaded region is where values of y can be.
Finally, a little more complex (the last problem):
.
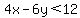
.
We can solve this for to make it easier for us to find the region where y is allowed to
exist just as we did before. We want to solve for +y. So let's multiply both sides of
the equation by -1. However, here's an important rule: whenever you multiply or divide both
sides of an inequality by a negative number, you must afterward reverse the direction of
the inequality.
.

.
Do the multiplication by -1 to get:
.
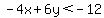
.
But don't forget that you have to reverse the direction of the inequality sign too. When
you do the inequality is now:
.
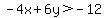
.
Now you can replace the inequality sign with an equal sign and solve the equation for y
just as you have always done. Begin by adding 4x to both sides to get:
.

.
Divide both sides by 6 to solve for y and get:
.

.
which becomes:
.

.
Graph this equation as you did previously. The slope is (2/3) and the y-axis intercept
is -2.
.
Now replace the = sign with the inequality sign pointing to the right so that the inequality
is now:
.
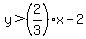
.
Again, shade the entire region ABOVE the graph of the right side of the equation.
That represents the place where y is allowed. y can NOT be on or below the graphed line.
.
After a little more practice you'll get familiar with this method and you can do things
faster and without thinking about it.
.
Hope this helps you with understanding the basic principles of doing problems such as
these inequalities.
|
|
|
| |