Question 663489: parallel to 2x + 4y = 5, passing through (1,2)
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
if line is parallel to  , will have same slope; so, let's find a slope , will have same slope; so, let's find a slope
 ....solve for ....solve for 


now we can find a line passing through ( , , ) and has a slope ) and has a slope  : :
| Solved by pluggable solver: FIND a line by slope and one point |
What we know about the line whose equation we are trying to find out:
- it goes through point (1, 2)
- it has a slope of -0.5
First, let's draw a diagram of the coordinate system with point (1, 2) plotted with a little blue dot:

Write this down: the formula for the equation, given point  and intercept a, is and intercept a, is
 (see a paragraph below explaining why this formula is correct) (see a paragraph below explaining why this formula is correct)
Given that a=-0.5, and  , we have the equation of the line: , we have the equation of the line:

Explanation: Why did we use formula  ? Explanation goes here. We are trying to find equation y=ax+b. The value of slope (a) is already given to us. We need to find b. If a point ( ? Explanation goes here. We are trying to find equation y=ax+b. The value of slope (a) is already given to us. We need to find b. If a point ( , , 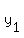 ) lies on the line, it means that it satisfies the equation of the line. So, our equation holds for ( ) lies on the line, it means that it satisfies the equation of the line. So, our equation holds for ( , , 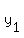 ): ):  Here, we know a, Here, we know a,  , and , and 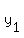 , and do not know b. It is easy to find out: , and do not know b. It is easy to find out:  . So, then, the equation of the line is: . So, then, the equation of the line is:  . .
Here's the graph:

|
|
|
|