|
Question 651682: a rocket weighs 6000 pounds when it is resting on the launch pad. the engines burn fuel at the rate of 20 pounds per second.
a. write a linear function W(t) expressing rocket weigh as a function of time t in seconds
b. at what time into the launch will the rocket weigh 40% of its original weight ?
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
a rocket weighs 6000 pounds when it is resting on the launch pad. the engines burn fuel at the rate of 20 pounds per second.
a. write a linear function W(t) expressing rocket weigh as a function of time t in seconds
Let x = t
Let y = W(t)
When x = 0, y = 6000
When x = 1, y = 5980, because it lost 20 pounds in 1 second
The problem now becomes the problem:
Find the equation of the line through the points (0,6000) and (1,5980)
1. find an equation of the line passing through the points
(0, 6000) and (1, 5980)
Slope formula
m =  with (x1, y1) = (0,6000) and (x2, y2) = (1, 5980)
m = with (x1, y1) = (0,6000) and (x2, y2) = (1, 5980)
m = 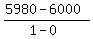 = = 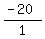 = -20
Point-slope formula:
y - y1 = m(x - x1)
y - 6000 = -20(x - 0)
y - 6000 = -20x
y = -20x + 6000
Now change y back to W(t) and x back to t
W(t) = -20t + 6000
-------------------------------------------
b. at what time into the launch will the rocket weigh 40% of its original weight ?
40% of 6000 is 0.4(6000) = 2400
We want to know t when W(t) = 2400, so we substitute
2400 for W(t) in
W(t) = -20t + 6000
2400 = -20t + 6000
20t = 3600
t = 180 seconds or 3 minutes.
Edwin = -20
Point-slope formula:
y - y1 = m(x - x1)
y - 6000 = -20(x - 0)
y - 6000 = -20x
y = -20x + 6000
Now change y back to W(t) and x back to t
W(t) = -20t + 6000
-------------------------------------------
b. at what time into the launch will the rocket weigh 40% of its original weight ?
40% of 6000 is 0.4(6000) = 2400
We want to know t when W(t) = 2400, so we substitute
2400 for W(t) in
W(t) = -20t + 6000
2400 = -20t + 6000
20t = 3600
t = 180 seconds or 3 minutes.
Edwin
|
|
|
| |