|
Question 647772: write an equation of a line containing the given point (8,-6) parallel to 2x-3y=7
Found 2 solutions by Algebraic, MathTherapy:
Answer by Algebraic(50)  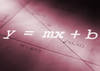 (Show Source): (Show Source):
You can put this solution on YOUR website! When you're given a specific point and an equation, you can use the point-slope formula to find a parallel line. REMEMBER: Parallel lines will always have the same slope as to what they gave you.
The point-slope formula is: y y1 = m(x x1)
First of all, the equation you provided is not in standard form. You need to put this equation in standard form to be able to obtain its slope.
The slope-intercept form (standard form) of an equation can be expressed as:

Step 1: We must put the equation they gave us in standard form, like the one that is above.
Original equation: 
You want to get 'y' by itself, so subtract '2x' from both sides.
Step 2: You'll get:

We want to get 'y' by itself, so divide 3 from the 'y' and from the rest of the equation.
Step 3: It becomes:

Step 4: The equation originally given is now in slope-intercept form, and we now know the slope is 
We know the slope stays the same as the original equation because parallel slopes stay exactly the same.
We now need to use the point-slope formula to find a parallel equation.
Let's recap.. the point-slope formula is: y y1 = m(x x1)
We're going to replace 'x1' with the 'x' coordinate given to us, the 'y1' with the 'y' coordinate given to us, and the m with the slope we just found.
Step 1:
Original point: (8,-6)
Slope: 
Let's begin by replacing the values in.
(y (-6)) = 2/3(x 8)
Step 2: Simplify the first parenthesis
(y + 6)) = 2/3(x 8)
Step 3: Distribute terms
(y + 6)) = ((2x/3) - (16/3))
Step 4: Combine like terms (You want to get 'y' by itself, so subtract 6 on both sides.)

Step 5: Find an LCD (least common denominator) that will divide into both denominators. The LCD is 3, so multiply 6 by 3 on the top and on the bottom.

Step 6: Combine like terms (subtract the fractions)

Your new parallel equation is: 
Answer by MathTherapy(10552)   (Show Source): (Show Source):
|
|
|
| |