|
Question 576707: how do you graph a line with the slope of -3 passing through the point (2,2)
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Graphs look are easier to draw, and look best on graph paper or grid paper. Having all those little squares helps a lot.
THE JUST DRAW APPROACH
Your first step may be to draw a set of x-y axes and plot the point (2,2).
(If you are lucky, the graph may turn out nice without too much work).
At the beginning it would look like this:
 Then you could use the slope to plot other points.
The slope is usually a rational number, like 3/5, or -2/7, or 1, or -3. That slope number is the ratio of "rise" (units moving up) to "run" (units moving to the right). A slope of 2/3 would mean that moving up 2 units and to the right 3 units you can locate another point.
For your line, a slope of -3=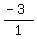 means that you move up by -3 units (meaning move down by 3 units) as you move right by 1 unit to locate the next point, like this (but do not draw the arrows):
 You can connect those two points with a straight line and hope for the best.
For a better graph, you may want to keep going like that, plotting more points, and/or reverse course and go in the opposite direction, plotting more points.
AT some point you may realize that it would be more convenient to have a different scale for your x and y axes. (I just did).
You may end up with something like this:
THE CAREFUL PLANNING APPROACH
You may want to make a table with x and y values, so you can carefully plan the scale on your x and y axes. It could be done as above, but you would calculate a bunch of points before plotting.
Starting with (x,y)=(2,2), you would add -3 to the y as you add 1 to the x to get points (3,-1), (4,-4), (5,-7), (6,-10).
Then you would go the opposite way adding 3 to the y as you add -1 to the x to get points (1,5), (0,8), (-1,11), (-2,14).
With all those points you would decide to draw the x axis from -2 to 6 and the y axis from -10 to 14, and then you may mark points (6,-10), and (-2,14), connect them with a straight line, verify that (2,2) is on that line, and congratulate yourself for a beautiful graph.
You could instead write the equation for the line (maybe in point-slope form), and pick your scales and end-points from there.
|
|
|
| |
