|
Question 552491: What is the general form of a line passing through (4,7) and has an an angle of 60degrees with the line x=4 ?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! see the diagram below:
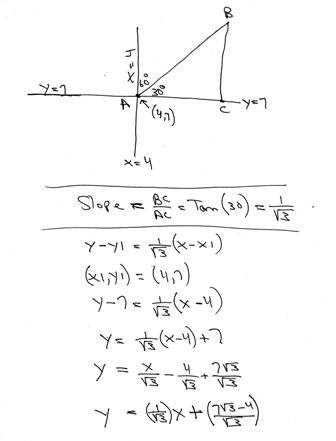
the line passes through the point (4,7) and is at an angle of 60 degrees with the line x = 4.
this makes it have a 30 degree angle with the line y = 7.
this makes the slope of this line equal to the tangent of 30 degrees which is equal to 1/sqrt(3).
we have the slope and we can find the equation of the line using the point slope form of that equation which is:
y - y1 = m(x - x1)
since we have (x1,y1) = 4,7), and we have m = (1/sqrt(3)), then the equation becomes:
y - 7 = (1/sqrt(3))(x - 4)
we now convert this equation into the slope intercept form of the equation of a straight line, which is:
y = mx + b
after conversion, our equation becomes:
y = (1/sqrt(3))x + (7*sqrt(3)-4)/sqrt(3)).
i confirmed that, when x = 4, y = 7, which shows that this line is passing through the point (4,7).
|
|
|
| |