|
Question 548646: Write an equation of the line that passes through the point (7, -6) and is perpendicular to the line 4x + 6y = 7
Answer by bucky(2189)   (Show Source):
You can put this solution on YOUR website! We were given the equation:
.
.
First, we need to find the slope of the graphed line that represents this equation. To do that, let's transform the given equation into the slope-intercept form 
.
Subtract 4x from both sides of the given equation. The result is:
.
.
Solve for y by dividing both sides (all terms) by 6
.
.
Note that the fraction (4/6) reduces to (2/3) when both the numerator and denominator are divided by 2. This makes the slope-intercept form become:
.
.
Here are the two critical things to this problem:
.
First, in the slope-intercept form of an equation, the multiplier of the x (called the coefficient of x) is the slope of the graphed line for that equation.
.
And second, any line perpendicular to the graphed line has a slope that is the negative and inverse of the slope for the graphed line.
.
So looking at the equation that we have in the slope-intercept form, we see that the slope for its graph is  because that is the multiplier of the x. (This -2/3 slope means that for every 3 units you move horizontally to the right in the x direction, the graph goes down 2 units in the y direction.)
.
Next we know that a line that is perpendicular to it will have a slope that is the negative of this (means change in sign) and is the inverse in value. (An inverse of an integer, means just put that integer as a denominator under a numerator of 1. So, for example, the inverse of 5 is  . For fractions, such as we have, we can quickly find the inverse by flipping the fraction upside down.) Applying these two characteristics, we see that the inverse of is 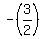 and then taking the negative of that changes it to positive. So we found that the slope of the line perpendicular to our given equation is  and it is the negative inverse of the slope of the given equation.
.
Let's put that into a slope-intercept form for the new equation we are getting for the perpendicular.
.
Again the basic slope intercept form is:
.
.
In which m (the multiplier of x) is the slope we want and b is the point where the graph for this equation crosses or intercepts the y-axis. So let's substitute the slope that we want into this equation to make it:
.
.
Next we make use of the fact that we want the graph of this equation to go through the given point (7, -6).
.
We know that the x value 7 and its corresponding y value -6 have to work in our equation, meaning that they have to be on the graphed line for this new equation. So we start with:
.
.
and substitute 7 for x and -6 for y to get:
.
.
Multiply out the fraction on the right side to get:
.
.
Solve for b by subtracting 21/2 from both sides as follows:
.
.
and  is the same as  so we can substitute that to get:
.
.
and combining the two fractions on the left side to get:
.
.
Now we can return to the equation we are finding:
.
.
and substitute -33/2 for b to get:
.
.
and that's the answer: the equation of the answer in slope intercept form for the perpendicular to the graph of the given equation.
.
We can convert this answer to the same form of the equation that we were given in the original problem. Begin by subtracting  from both sides to get:
.
.
Then you can get rid of the denominator 2 by multiplying all term on both sides of this equation by 2 to get:
.
.
The graph of these two equations, the original equation and the equation for the perpendicular to it that goes through (7, -6) is shown below:
.
.
The red graph is for the original equation we were given, and the green graph is the graph of the equation that we developed for its perpendicular. As a check, you should be able to see that the point (7, -6) is on the green graph of the perpendicular.
.
Hope this helps you to understand how to find perpendiculars to the graphs of equations that you are given.
.
|
|
|
| |
