How do you get the equation of a line perpendicular to the line whose equation
is y=6 which passes through (-3,3)?
Please explain each step because I'm really confused.
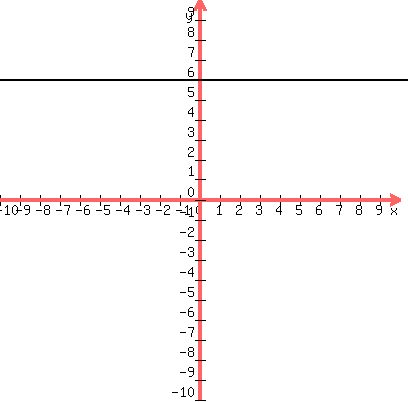
First we must know what line the equation y = 6 is the equation of.
Notice that the equation
y = 6
is the same as if it were
y = 0x + 6
because the term 0x is just zero and has no effect when + 6 is added to it.
However when it is written as
y = 0x + 6 instead of just y = 6, it looks like
y = mx + b
and has a y intercept of (0,6) and has a slope of m=0, which means
that it is horizontal, goes through (0,6) and looks like this:
Now we want the equation of a line that is perpendicular to that one,
and which passes through the point (-3,3).
To be perpendicular to a horizontal line, a line must be vertical,
like this green vertical line which, as you see, passes through the
point (-3,3):
Now vertical lines do not have slopes, so we cannot use any of the
ordinary methods to find the equation of a vertical line. To get
the equation of a vertical line, we must look at what is true about
every point on that vertical line. Let's look at some arbitrary
points on that green line and see what is true about all of them:
Now what do you notice that is in common with all those points:
(-3,9),(-3,8),(-3,5),(-3,3),(-3,-5),(-3,-7),(-3,-2) ?
Every one of them has their x-coordinate equal to -3. Therefore
the equation of that green vertical line is one that tells that fact,
that all the x's are equal to -3, which is this very simple equation:
x = -3
That is the equation of that green line because it tells us that all
the x-coordinates of the points on it are -3, and no other line has that
property.
Edwin
