Question 539531: what is the equation of the perpendicular bisector of ab if a(12,-2) and b(20,-6)
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! If the coordinates of A and B are ( x1, y1) and ( x2, y2) respectively, then the midpoint, M, of AB is given by the following formula
( 12 , -2 ) ( 20 , -6 )
M(x,y) = 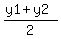
x= ( 12 + 20 )/ 2 y= ( -2 -6 )/ 2
x= 16 ,y= -4
The slope of this line
x1 y1 x2 y2
12 * -2 20 -6
slope m = (y2-y1)/(x2-x1)
( -6 - -2 )/( 20 - 12 )
( -4 / 8 )
m= - 1/ 2
The line perpendicular to this line will have a slope of 2 and passing through (16,-4)
m= 2
Plug value of the slope and point ( 16 , -4 ) in
Y = m x + b
-4.00 = 32 + b
b= -4 - 32
b= -36
So the equation will be
Y = 2 x -36
m.ananth@hotmail.ca
|
|
|