SOLUTION: x(y+z)=6 y(z+x)=10 z(x+y)=12 find the value of x,y,z

x(y+z)=6
y(z+x)=10
z(x+y)=12

xy + xz =  6
yz + xy = 10
xz + yz = 12


xy + xz     =   6
xy      + yz = 10
     xz + yz = 12

Let xy = a, xz = b and yz = c

a + b     =  6
a     + c = 10
    b + c = 12

Solve that system and get a = 2, b = 4, c = 8

Then xy = a = 2, xz = b = 4 and yz = c = 8

We now have this system:

xy = 2, xz = 4, yz = 8

Solve the first one for y, y =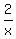 

Sunstitute in the third equation:

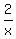z = 8

Multiply through by x

2z = 8x

 z = 4x

Substitute in xz = 4

x(4x) = 4

  4x² = 4
   x² = 1
    x = ±1

Substitute in  z = 4x

   z = 4(±1)
   z = ±4

Substitute in y =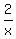 
  
   y = 
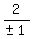   y = ±2

(x,y,z) = (±1,±2,±4)

Two solutions:  (x,y,z) = (1,2,4) and (x,y,z) = (-1,-2,-4)

Edwin