SOLUTION: Solve using the elimination method. Show your work. If the system has no solution or an infinite number of solutions, state this. 4x – 8y = 48 11x + 3y = -105.5

 4x – 8y =   48 
11x + 3y = -105.5 

We start by eliminating y:

Look at the absolute values of the coefficients of x
|4| = 4, |11| = 11

The least common multiple of of 4 and 11 is 44.  So if
we multiply the first equation through by -11 the 
coefficient of y will be -44, and if we multiply
the second equation through by 4, the coefficient
of y will be +44, and the x-terms will cancel when adding
the equations term by term.

-44x + 88y = -528 
 44x + 12y = -422
-----------------
      100y = -950
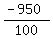         y = 
         y =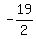 

Now we start over and this time we eliminate y: 

 4x – 8y =   48 
11x + 3y = -105.5

Look at the absolute values of the coefficients of y
|-8| = 8, |3| = 3

The least common multiple of of 8 and 3 is 24.  So if
we multiply the first equation through by 3 the 
coefficient of y will be -24, and if we multiply
the second equation through by 8, the coefficient
of y will be +24, and the terms will cancel when adding
the equtions term by term.

 12x - 24y =  144
 88x + 24y = -844
-----------------
100x       = -700
         x =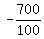 
         x = -7

So the solution is (x,y) = (-7,)

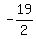Edwin