SOLUTION: You have two tanks used to store water. A 50 gallon tank is empty and then is filled at a rate of 2 gallons per minute. At the exact same time, a 140 gallon tank starts out complet

For the first (smaller) tank that starts out empty,

let x = the time in minutes
Let y = the amount of water in gallons in the smaller tank at time x

When the time = 0 minutes, the amount of water in the 
50 gallon tank is 0 gallons.

Therefore when x = 0, y = 0.

When the time = 1 minute, the amount of water in the 
50 gallon tank is 2 gallons.

Therefore when x = 1, y = 2.

Let's find the equation of the line that goes through the points
(0,0) and (1,2)

m = 

m = 

m = 

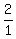m = 2





Here is the graph of the water in the smaller tank,
which is full after 25 minutes.  It is the green line.
Notice that the green line goes upward to the right 
indicating that the smaller tank is filling up.

 

Let's do the same thing with the larger tank, the one that starts
out full.

let x = the time in minutes
Let y = the amount of water in gallons in the large tank at time x

When the time = 0 minutes, the amount of water in the 
140 gallon tank is 140 gallons.

Therefore when x = 0, y = 140.

When the time = 1 minute, the amount of water in the 
140 gallon tank is 135 gallons, for it has lost 5 gallons

Therefore when x = 1, y = 135.

Let's find the equation of the line that goes through the points
(0,140) and (1,135)

m = 

m = 

m = 

m = -5






Here is the graph of the water in the larger tank,
which is empty after after 28 minutes.  It is the blue line.
Notice that the blue line goes downward to the right 
indicating that the larger tank is emptying.






We want to know where these two lines intersect for that point
will tell us when the two tanks have the same amount of water:

Now we have this system of equations:



We solve that by substitution and get 

x = 20, y = 40

Which means when exactly 20 minutes have lapsed, both
tanks contain 40 gallons.

Checking: The smaller tank has gained 40 gallons in 20 minutes
since it gaine 2 gallons per minute.  The larger tank has lost
100 gallons in 20 minutes since it loses 5 gallons per minute,
so it only has 40 gallons left in it.

 


Edwin