|
Question 508363: If the slope of ab is 3, which is the value of y? A(4,Y) B(2,1)
Found 2 solutions by Maths68, Theo:
Answer by Maths68(1474)   (Show Source): (Show Source):
You can put this solution on YOUR website! Equation of the line point-slope form
m=(y2-y1)/(x2-x1)
A (4, y) and B (2, 1)
slope = m = 3
m=(y2-y1)/(x2-x1)
3=(1-y) /(2- 4)
3=(1-y) /(-2)
(-2)*3=1-y
-6=1-y
-6-1=-y
-7=-y
Multiply above equation by -1
7=y
y=7
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! 2 points are (4,y), (2,1)
let (x1,y1) = (2,1)
let (x2,y2) = 4,y)
formula for slope is (y2-y1)/x2-x1)
slope is equal to 3 so formula becomes:
(y2-y1)/(x2-x1) = 3
replace x1,x2,y1,y2 with their values to get:
(y-1)/(4-2) = 3
simplify to get:
(y-1)/2 = 3
multiply both sides of this equation by 2 to get:
y-1 = 6
add 1 to both sides of this equation to get:
y = 7
that should be your answer.
your points are:
A(4,7), B(2,1)
if you let B = (x1,y1) and you let A = (x2,y2) then slope is equal to:
(y2-y1)/x2-x1) = 6/2 = 3
slope checks out so the value of y is good.
you can solve for the y-intercept by replacing x and y in the slope intercept form of the equation of a straight line to get:
y = mx + b (slope intercept form of straight line linear equation)
replace m with 3 to get:
y = 3x + b
replace x and y with 2 and 1 to get
1 = 3*2) + b
simplify to get:
1 = 6 + b
subtract 6 from both sides of the equation to get:
b = -5
equation becomes:
y = 3x - 5
a graph of your equation is shown below:
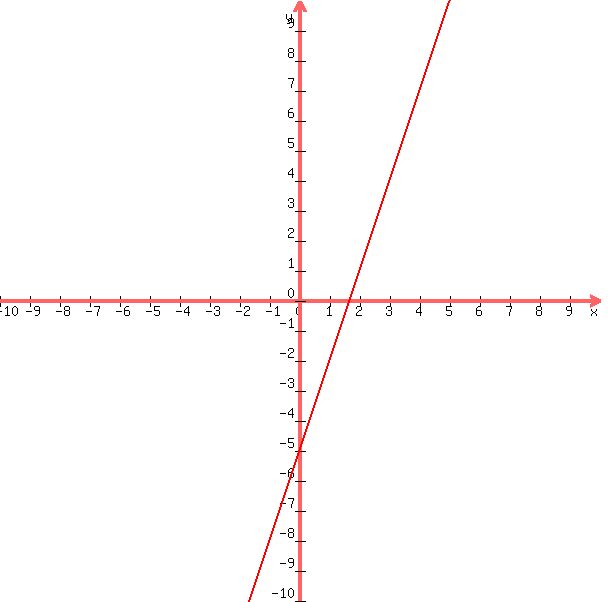
a table of some of the values of x and their corresponding values of y will show that the change in x of 1 unit results in a change in y of 3 units.
it also shows that when x = 0, y = -5 which makes -5 the y intercept of the equation.
x y change in x change in y
0 -5 n/a n/a
1 -2 1 3
2 1 1 3
3 4 1 3
4 7 1 3
|
|
|
| |