a) y=3x+1
b) 3x-4y=12
I'll do the second one first, since it requires more work,
then I'll do the first one:
Solve it for y:
3x - 4y = 12
-4y = -3x + 12
Divide through by 4
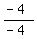 y =
y = 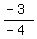 x +
x + 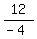 y =
y =  x - 3
compare that to
y = mx + b
the slope m is
x - 3
compare that to
y = mx + b
the slope m is  and the y-intercept is (0,b) or (0,-3)
We begin at the y-intercept (0,-3):
and the y-intercept is (0,b) or (0,-3)
We begin at the y-intercept (0,-3):
 We take the numerator of the slope which is 3, and since the
slope is positive we draw a line from the y-intercept UPWARD
3 units, like the green arrow below. [If the slope had been
negative, which it wasn't, we would have draw the arrow downward]
We take the numerator of the slope which is 3, and since the
slope is positive we draw a line from the y-intercept UPWARD
3 units, like the green arrow below. [If the slope had been
negative, which it wasn't, we would have draw the arrow downward]
 Now we take the denominator of the slope which is 4, and draw a
another line from that green arrow head to the RIGHT 4 units, as
shown below. [Even if the slope had been negative, we still would have
drawn the arrow to the RIGHT the number of units indicated by the
denominator of the slope.]
Now we take the denominator of the slope which is 4, and draw a
another line from that green arrow head to the RIGHT 4 units, as
shown below. [Even if the slope had been negative, we still would have
drawn the arrow to the RIGHT the number of units indicated by the
denominator of the slope.]
 Now get a ruler or straight edge and draw a straight line
through the y-intercept (0,-3) and through the second arrow head:
Now get a ruler or straight edge and draw a straight line
through the y-intercept (0,-3) and through the second arrow head:
 -----------------------------
Now I'll do the first one:
y = 3x + 1
It is already solved for y and is in slope-y-intercept form,
so we don't have to do that like we did in the other one:
compare that to
y = mx + b
the slope m is 3 and the y-intercept is (0,b) or (0,1)
As before we begin at the y-intercept (0,1):
-----------------------------
Now I'll do the first one:
y = 3x + 1
It is already solved for y and is in slope-y-intercept form,
so we don't have to do that like we did in the other one:
compare that to
y = mx + b
the slope m is 3 and the y-intercept is (0,b) or (0,1)
As before we begin at the y-intercept (0,1):
 Now the slope 3 in this one doesn't have a visible denominator,
so we write it as
Now the slope 3 in this one doesn't have a visible denominator,
so we write it as 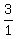 so it will have both a numerator and
a denominator:
We take the numerator of the slope which is 3, and since the
slope is positive we draw a line from the y-intercept UPWARD
3 units, like the green arrow below. [If the slope had been
negative, which it wasn't, we would have draw the arrow downward]
so it will have both a numerator and
a denominator:
We take the numerator of the slope which is 3, and since the
slope is positive we draw a line from the y-intercept UPWARD
3 units, like the green arrow below. [If the slope had been
negative, which it wasn't, we would have draw the arrow downward]
 Now we take the denominator of the slope which is 1, and draw a
another line from that green arrow head to the RIGHT 1 unit, as
shown below. [Even if the slope had been negative, we still would have
drawn the arrow to the RIGHT the number of units indicated by the
denominator of the slope.]
Now we take the denominator of the slope which is 1, and draw a
another line from that green arrow head to the RIGHT 1 unit, as
shown below. [Even if the slope had been negative, we still would have
drawn the arrow to the RIGHT the number of units indicated by the
denominator of the slope.]
 Now get a ruler or straight edge and draw a straight line
through the y-intercept (0,1) and through the second arrow head:
Now get a ruler or straight edge and draw a straight line
through the y-intercept (0,1) and through the second arrow head:
 Edwin
Edwin