|
Question 448805: graph the line that goes through point (3,8) and is parallel to the line whose equation is 6y-10x=30
Found 2 solutions by mananth, ikleyn:
Answer by mananth(16949)   (Show Source):
You can put this solution on YOUR website! (3,8) and is parallel to the line whose equation is 6y-10x=30
-10x+6y=30
Find the slope of this line
y=10x+30
Divide by 6
y=1.67x +5
Compare this equation with y=mx+b
slope m = 1.67
The slope of a line parallel to the above line will be the same
The slope of the required line will be 1.67
m= 1.67 ,point (3,8)
Find b by plugging the values of m & the point in
y=mx+b
8=5.00+b
b=3
m=1.67
Plug value of the slope and b
The required equation is y=1.67 x+3
...
y=1.67 x+3
when x= 0 y= 3 ( 0 , 3 )
when y = 0 x= -1.8 ( -1.8 , 0 )
Answer by ikleyn(53612)  (Show Source):
You can put this solution on YOUR website! .
Graph the line that goes through point (3,8) and is parallel to the line whose equation is 6y-10x=30
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @mananth is incorrect.
His final equation y = 1.67x + 3 is incorrect.
The point (3,8) does not lie on this line.
Indeed, the left side 'y' at this point is 1.67*3 + 3 = 8.01, but not 8, as it should be.
See my correct solution below.
An equation for the line parallel to 6y - 10x = 30 is
6y - 10x = c,
where 'c' is some constant.
We find 'c' by substituting the coordinates x= 3, y= 8 into this equation
c = 6*8 - 10*s = 18.
Thus an equation is 6y - 10x = 18.
In the slope-intercept form it is y = 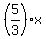 + 3, which is different from the equation found by @mananth.
Solved correctly.
Simply IGNORE the post by @mananth, since his solution is wrong.
----------------------------
Not only this particular problem is solved incorrectly by @mananth.
Many other similar problems were solved incorrectly by @mananth.
Incorrectly solved are ALL similar problem, where coefficients of linear equations
are / (should be) rational numbers, which can not be presented as finite decimal fractions.
Then @mananth, by applying his incorrect algorithm of rounding, makes everything wrong.
Rounding in such situations IS NOT ALLOWED.
|
|
|
| |
