|
Question 446122: If an object is tossed into the air the path of this object is represented by the equation atē+bt+c=h where h is the height after t seconds, a is the acceleration due to gravity, b is the initial velocity, and c is the initial height.
a.A rocket is thrust vertically upward from the top of a tower 80 feet tall, with an initial velocity of 64 ft/s, (the acceleration due to gravity is -16ft/sec). Write the quadratic equation representing this scenario when h is 0.
b.Find the roots (solutions) for this quadratic equation, solving by factoring.
c.How high will the rocket be after 3 seconds?
d.How long will it take for the rocket to hit the ground?
How long will it take for the rocket to hit the ground?
Given the graph of the equation, identify and appropriately label, the vertex, solutions or roots, all intercepts, and axis of symmetry.
Given the graph of the equation, identify and appropriately label, the vertex, solutions or roots, all intercepts, and axis of symmetry.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! If an object is tossed into the air the path of this object is represented by the
equation atē+bt+c=h where h is the height after t seconds, a is the acceleration
due to gravity, b is the initial velocity, and c is the initial height.
:
a.A rocket is thrust vertically upward from the top of a tower 80 feet tall,
with an initial velocity of 64 ft/s, (the acceleration due to gravity is -16ft/sec).
Write the quadratic equation representing this scenario when h is 0.
-16t^2 + 64t + 80 = 0
:
b.Find the roots (solutions) for this quadratic equation, solving by factoring.
-16t^2 + 64t + 80 = 0
Simplify, divide by -16, (makes it easier to factor), results:
t^2 - 4t - 5 = 0
factors to
(t-5)(t+1) = 0
Roots
t=+5
t=-1
:
c.How high will the rocket be after 3 seconds?
Replace t with 3 in the original equation
h = -16(3^2) + 64(3) + 80
h = -16(9) + 192 + 80
h = -144 + 192 + 80
h = 128 ft after 3 sec
:
d.How long will it take for the rocket to hit the ground?
the positive root: t=5 sec, then h=0, which is the ground
:
Given the graph of the equation, identify and appropriately label, the vertex, solutions or roots, all intercepts, and axis of symmetry.
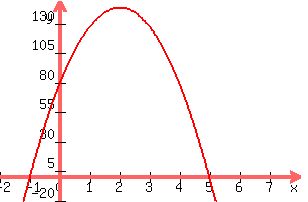
You can see on the graph, the x intercepts, -1 and +5, y intercept y=80
Vertex: x=2, y=144 Axis of symmetry: x=2
|
|
|
| |